HistogramTransformInterpolation
HistogramTransformInterpolation[{x1,x2,…}]
求使得变换后的值 ![]() 接近均匀分布的函数
接近均匀分布的函数 ![]() .
.
HistogramTransformInterpolation[{x1,x2,…},ref]
求使得 ![]() 服从分布 ref 的
服从分布 ref 的 ![]() .
.
HistogramTransformInterpolation[{x1,x2,…},ref,n]
求具有 n 个等距分位数的函数.
HistogramTransformInterpolation[image,…]
求改变 image 直方图形状的函数.
更多信息

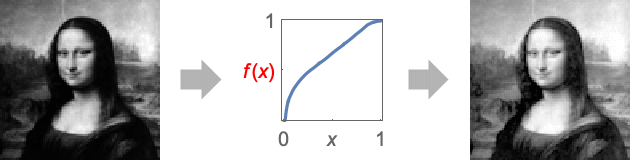
- HistogramTransformInterpolation 返回一个函数,通过改变图像直方图的形状进行直方图变换,通常用于直方图均衡化或直方图匹配.
- HistogramTransformInterpolation 返回一个函数 f 或每个通道的函数列表,每个函数用一个 InterpolatingFunction 表示.
- 使用 HistogramTransform 可通过相应函数进行直方图转换.
- HistogramTransformInterpolation[image] 实际上是像素值的累积分布 (CDF). 应用于像素值时,它将创建具有几乎平坦的直方图的图像.
- HistogramTransformInterpolation[image,ref] 求使转换后的像素值具有与 ref 几乎相同分布的函数.
- 参考 ref 可以是另一幅图像、数据集或一个分布.
- HistogramTransformInterpolation 适用于三维以及二维图像,也适用于任意阶数的数据集的列表.
- HistogramTransformInterpolation[{data1,data2,…},…] 给出对应于每个数据集的函数列表.
- 对于 HistogramTransformInterpolation[image,ref],将使用 256 个分位数.
- 参数设置为 HistogramTransformInterpolation[data,ref,Automatic] 时,分位数的数目与 Histogram[data] 中所用的组数相同.
范例
打开所有单元关闭所有单元应用 (1)
属性和关系 (2)
HistogramTransformInterpolation 可用来获取 HistogramTransform 中使用的变换函数:
当存在时,HistogramTransformInterpolation 的结果是解析解的近似:
文本
Wolfram Research (2012),HistogramTransformInterpolation,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html (更新于 2014 年).
CMS
Wolfram 语言. 2012. "HistogramTransformInterpolation." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html.
APA
Wolfram 语言. (2012). HistogramTransformInterpolation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HistogramTransformInterpolation.html 年