HoeffdingD[v1,v2]
gives Hoeffding's dependence measure for the vectors v1 and v2.
HoeffdingD[m]
gives Hoeffding's dependence measure for the matrix m.
HoeffdingD[m1,m2]
gives Hoeffding's dependence measure for the matrices m1 and m2.
HoeffdingD[dist]
gives Hoeffding's matrix for the multivariate symbolic distribution dist.
HoeffdingD[dist,i,j]
gives the ![]()
![]() element of for the multivariate symbolic distribution dist.
element of for the multivariate symbolic distribution dist.


HoeffdingD
HoeffdingD[v1,v2]
gives Hoeffding's dependence measure for the vectors v1 and v2.
HoeffdingD[m]
gives Hoeffding's dependence measure for the matrix m.
HoeffdingD[m1,m2]
gives Hoeffding's dependence measure for the matrices m1 and m2.
HoeffdingD[dist]
gives Hoeffding's matrix for the multivariate symbolic distribution dist.
HoeffdingD[dist,i,j]
gives the ![]()
![]() element of for the multivariate symbolic distribution dist.
element of for the multivariate symbolic distribution dist.
Details

- HoeffdingD[v1,v2] gives Hoeffding's dependence measure between v1 and v2.
- Hoeffding's is a measure of dependence based on the relative order of elements in the two lists.
- Hoeffding's between v1 and v2 is given by
![30 (-2 (n-2) R+(n-3) (n-2) S+Q)/TemplateBox[{{n, -, 4}, 5}, Pochhammer] 30 (-2 (n-2) R+(n-3) (n-2) S+Q)/TemplateBox[{{n, -, 4}, 5}, Pochhammer]](Files/HoeffdingD.en/3.png) , where
, where 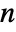 is the number of observations in v1,
is the number of observations in v1, 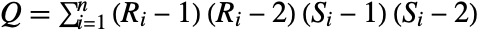 ,
, 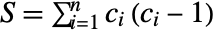 ,
, 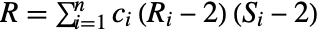 ,
, 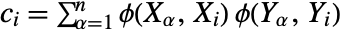 for
for 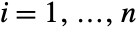 ,
,  is the rank of v1i,
is the rank of v1i, 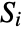 is the rank of v2i, and
is the rank of v2i, and 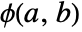 is equal to Boole[a<b].
is equal to Boole[a<b]. - The arguments v1 and v2 can be any real‐valued vectors of equal length greater than 5.
- For a matrix m with
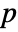 columns, HoeffdingD[m] is a
columns, HoeffdingD[m] is a 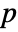 ×
×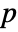 matrix of the dependence measures between columns of m.
matrix of the dependence measures between columns of m. - For an
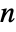 ×
×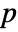 matrix m1 and an
matrix m1 and an 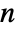 ×
×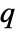 matrix m2, HoeffdingD[m1,m2] is a
matrix m2, HoeffdingD[m1,m2] is a 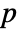 ×
×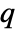 matrix of the dependence measures between columns of m1 and columns of m2.
matrix of the dependence measures between columns of m1 and columns of m2. - HoeffdingD[dist,i,j] is given by 30 Expectation[(F[x,y]-G[x]H[y])^2,{x,y}disti,j], where F[x,y], G[x], and H[y] are the CDFs of the
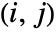
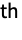 ,
, 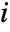
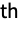 , and
, and 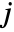
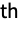 marginals of dist respectively.
marginals of dist respectively. - HoeffdingD[dist] gives a matrix where the
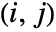
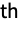 entry is given by HoeffdingD[dist,i,j].
entry is given by HoeffdingD[dist,i,j].
Examples
open all close allBasic Examples (4)
Scope (7)
Data (4)
Exact input yields exact output:
Approximate input yields approximate output:
SparseArray data can be used:
Applications (3)
Hoeffding's is typically used to detect non-monotonic dependency structures:
Hoeffding's tends to be larger for dependent vectors:
The value tends to 0 for independent vectors:
Hoeffding's can detect linear dependence:
SpearmanRho and KendallTau are more sensitive to linear dependence:
Hoeffding's can also detect many types of nonlinear dependence:
Use HoeffdingDTest to determine if the value is statistically significant:
Related Guides
History
Text
Wolfram Research (2012), HoeffdingD, Wolfram Language function, https://reference.wolfram.com/language/ref/HoeffdingD.html.
CMS
Wolfram Language. 2012. "HoeffdingD." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HoeffdingD.html.
APA
Wolfram Language. (2012). HoeffdingD. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HoeffdingD.html
BibTeX
@misc{reference.wolfram_2025_hoeffdingd, author="Wolfram Research", title="{HoeffdingD}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/HoeffdingD.html}", note=[Accessed: 08-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_hoeffdingd, organization={Wolfram Research}, title={HoeffdingD}, year={2012}, url={https://reference.wolfram.com/language/ref/HoeffdingD.html}, note=[Accessed: 08-January-2026]}