WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

BlomqvistBeta
✖
BlomqvistBeta

✖
BlomqvistBeta[v1,v2]

gives Blomqvist's medial correlation coefficient β for the vectors v1 and v2.

✖

gives Blomqvist's medial correlation coefficient β for the matrix m.

✖
BlomqvistBeta[m1,m2]

gives Blomqvist's medial correlation coefficient β for the matrices m1 and m2.

✖

gives the medial correlation coefficient matrix for the multivariate symbolic distribution dist.

✖
BlomqvistBeta[dist,i,j]

gives the (i,j)^(th) medial correlation coefficient for the multivariate symbolic distribution dist.

Details

  • BlomqvistBeta[v1,v2] gives Blomqvist's medial correlation coefficient β between v1 and v2.
  • Blomqvist's β between vectors x and y is given by Correlation[Sign[x-μx],Sign[y-μy]], where μx and μy are the medians of x and y, respectively.
  • The arguments v1 and v2 can be any real‐valued vectors of equal length.
  • For a matrix m with 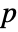columns BlomqvistBeta[m] is a 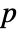× 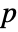matrix of the β's between columns of m.
  • For an 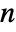× 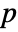matrix m1 and an 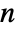× 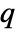matrix m2 BlomqvistBeta[m1,m2] is a 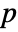× 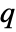matrix of the β's between columns of m1 and columns of m2.
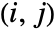
  • BlomqvistBeta[dist,i,j] is Probability[(x-μx)(y-μy)>0,{x,y}disti,j]-Probability[(x-μx)(y-μy)<0,{x,y}disti,j] where disti,j is the 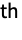^(th) marginal of dist.
  • BlomqvistBeta is not well defined for discrete distributions or in the presence of ties.
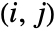
  • BlomqvistBeta[dist] gives a matrix β where the 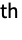^(th) entry is given by BlomqvistBeta[dist,i,j].

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Blomqvist's β for two vectors:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-gugb6d
In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-fulot0
Out[3]=3

Blomqvist's β for a matrix:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-9un6t
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-hz9gv1

Blomqvist's β for two matrices:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-bv14aj
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-ce2wv
In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-i51zwj

Compute Blomqvist's β matrix for a bivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-f7dh9d
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-mzz2lg

Compare to a simulated value:

In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-nwpxl1

Scope  (7)Survey of the scope of standard use cases

Data  (4)

Exact input yields exact output:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-eta06h
Out[1]=1

Approximate input yields approximate output:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-bbwiw5
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-bamv3h
Out[2]=2

Works with large arrays:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-kt50m4
Out[1]=1

SparseArray data can be used:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-cz9dkm

Distributions and Processes  (3)

Blomqvist's β matrix for a continuous multivariate distribution:

In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-fnv00k
In[4]:=4
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-tekwa
Out[4]=4

Blomqvist's β matrix for derived distributions:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-c3a9y
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-cy97of
In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-etkwz

Data distribution:

In[4]:=4
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-hxjash
In[5]:=5
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-gm1a47
In[6]:=6
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-edj4ah

Blomqvist's β matrix for a random process at times and :

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-hv1ygl

Applications  (3)Sample problems that can be solved with this function

Blomqvist's β is typically used to detect linear dependence between two vectors:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-ieb3ez

The absolute magnitude of β tends to 1 given strong linear dependence:

In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-eovfow
Out[3]=3

The value tends to 0 for linearly independent vectors:

In[4]:=4
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-csoxzv
Out[4]=4

Blomqvist's β can be used to measure linear association:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-g4uich
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-f44cf5
Out[2]=2

Blomqvist's β only detects monotonic dependence structures:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-7nvfr
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-nazb6e
In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-j9qi3
In[4]:=4
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-gtfa0z
Out[4]=4

HoeffdingD can be used for a variety of other dependence structures:

In[5]:=5
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-jor85u
Out[5]=5

Properties & Relations  (7)Properties of the function, and connections to other functions

Blomqvist's β ranges from to for high negative and high positive association, respectively:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-cishqp
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-cp90d4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-mp4oro
Out[3]=3

Blomqvist's β matrix is symmetric:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-31bc2
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-mmzf9d
Out[2]=2

The diagonal elements of Blomqvist's β matrix are 1:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-o1vsb7
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-h7qlge
Out[2]=2

Blomqvist's for even sample sizes:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-iwlpup
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-qubvni
Out[2]=2

Median-centered data:

In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-dziua2
In[4]:=4
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-gn688l
Out[4]=4

Count the number of points in each quadrant:

In[5]:=5
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-3rmyw
In[6]:=6
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-hkz0p3
Out[6]=6
In[7]:=7
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-coibfl
Out[7]=7

Blomqvist's β:

In[8]:=8
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-fflt44
Out[8]=8
In[9]:=9
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-cimejn
Out[9]=9

Blomqvist's β will yield or if there is perfect monotonic association:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-by9rj0
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-gyt4k
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-gdt5ie
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-ckj7he
Out[4]=4

This is in contrast to Correlation, which measures the degree of linear association:

In[5]:=5
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-7kt18
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-m7fz8x
Out[6]=6

BlomqvistBetaTest can be used to test the value of β:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-p2yi95
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-cdzlve
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-cye8gw
Out[3]=3

IndependenceTest can be used to automatically select an appropriate test:

In[4]:=4
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-gpn0r
Out[4]=4

Blomqvist's β for a bivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-bfewud
In[2]:=2
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-ewdode
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-gd8n5r
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-grblhu
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-fy88em
In[6]:=6
✖
https://wolfram.com/xid/0hyyfta78qi50wq7-n4qnp
Out[6]=6
Wolfram Research (2012), BlomqvistBeta, Wolfram Language function, https://reference.wolfram.com/language/ref/BlomqvistBeta.html.
✖
Wolfram Research (2012), BlomqvistBeta, Wolfram Language function, https://reference.wolfram.com/language/ref/BlomqvistBeta.html.

Text

Wolfram Research (2012), BlomqvistBeta, Wolfram Language function, https://reference.wolfram.com/language/ref/BlomqvistBeta.html.

✖
Wolfram Research (2012), BlomqvistBeta, Wolfram Language function, https://reference.wolfram.com/language/ref/BlomqvistBeta.html.

CMS

Wolfram Language. 2012. "BlomqvistBeta." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BlomqvistBeta.html.

✖
Wolfram Language. 2012. "BlomqvistBeta." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BlomqvistBeta.html.

APA

Wolfram Language. (2012). BlomqvistBeta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BlomqvistBeta.html

✖
Wolfram Language. (2012). BlomqvistBeta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BlomqvistBeta.html

BibTeX

@misc{reference.wolfram_2025_blomqvistbeta, author="Wolfram Research", title="{BlomqvistBeta}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/BlomqvistBeta.html}", note=[Accessed: 29-March-2025 ]}

✖
@misc{reference.wolfram_2025_blomqvistbeta, author="Wolfram Research", title="{BlomqvistBeta}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/BlomqvistBeta.html}", note=[Accessed: 29-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_blomqvistbeta, organization={Wolfram Research}, title={BlomqvistBeta}, year={2012}, url={https://reference.wolfram.com/language/ref/BlomqvistBeta.html}, note=[Accessed: 29-March-2025 ]}

✖
@online{reference.wolfram_2025_blomqvistbeta, organization={Wolfram Research}, title={BlomqvistBeta}, year={2012}, url={https://reference.wolfram.com/language/ref/BlomqvistBeta.html}, note=[Accessed: 29-March-2025 ]}