WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

HoeffdingD

HoeffdingD[v₁,v₂]

ベクトル v₁と v₂についてのHoeffdingの依存性尺度  を返す．

行列 m についてのHoeffdingの依存性尺度  を返す．

HoeffdingD[m₁,m₂]

行列 m₁ と m₂ についてのHoeffdingの依存性尺度  を返す．

HoeffdingD[dist]

多変量記号分布 dist についてのHoeffdingの依存性尺度  を返す．

HoeffdingD[dist,i,j]

多変量記号分布 dist についてのHoeffdingの依存性尺度  の番目の項目を返す．

詳細

HoeffdingD[v₁,v₂]は v₁と v₂の間のHoeffdingの依存性尺度  を返す．
Hoeffdingの  は2つのリストの要素の相対的な順序に基づく依存性の尺度である．
v₁ と v₂の間のHoeffdingの  はで与えられる．ただし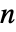，は v₁における観測数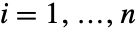，のときに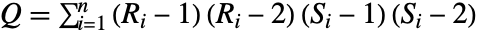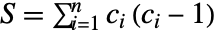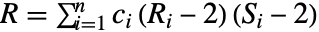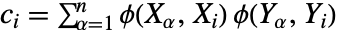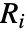，, ，，は v_1iの順位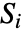，は v_2i の順位で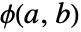はBoole[a<b]に等しい．
引数 v₁と v₂ は5より大きく長さが等しい任意の実ベクトルである．
列数が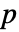の行列 m についてHoeffdingD[m]は m の列間の依存性尺度の 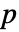× 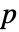行列である．
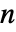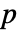× 行列 m₁と 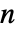× 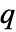行列 m₂について，HoeffdingD[m₁,m₂]は m₁の列と m₂の列の間の依存性尺度の 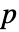× 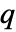行列である．
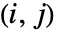
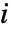HoeffdingD[dist,i,j]はF[x,y]， G[x]，H[y]が，それぞれ dist の，番目，番目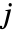，番目の周辺分布である30 Expectation[(F[x,y]-G[x]H[y])^2,{x,y}dist_i,j]で与えられる．
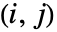
HoeffdingD[dist]は行列  を与える．ここで，番目の項目はHoeffdingD[dist,i,j]で与えられる．

例題

すべて開くすべて閉じる

例 (4)

2つのベクトルのためのHoeffdingの ：

行列のためのHoeffdingの ：

2つの行列のためのHoeffdingの ：

二変量分布のためのHoeffdingの  を計算する：

シミュレーションによる値と比較する：

スコープ (7)

データ (4)

厳密な入力は厳密な出力を与える：

近似入力は近似出力を与える：

大規模配列に使うことができる：

SparseArrayデータを使うことができる：

分布と過程 (3)

多変量連続分布についてのHoeffdingの  行列：

派生分布についてのHoeffdingの  行列：

データ分布について：

時間およびのランダム過程についてのHoeffdingの  行列：

アプリケーション (3)

Hoeffdingの  は，一般に非単調依存構造の検出に使われる：

Hoeffdingの  は従属ベクトルについては大きくなる傾向がある：

独立ベクトルの場合は値がゼロに近くなる：

Hoeffdingの  で線形従属性を検出することができる：

SpearmanRhoおよびKendallTauは，線形従属性に対してより敏感である：

Hoeffdingの  は，多くの非線形従属性も検出することができる：

HoeffdingDTestを使って値が統計的に有意かどうか確かめる：

特性と関係 (4)

大きいHoeffdingの  の値は従属性が大きくなっていることを示す：

Hoeffdingの  行列は対称行列である：

Hoeffdingの  行列の対角要素は1である：

二変量連続分布のHoeffdingの ：

トップへ