Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

HoeffdingD

HoeffdingD[v₁,v₂]

给出向量 v₁ 和 v₂ 的 Hoeffding 相关性度量 .

给出矩阵 m 的 Hoeffding 相关性度量 .

HoeffdingD[m₁,m₂]

给出矩阵 m₁ 和 m₂ 的 Hoeffding 相关性度量 .

HoeffdingD[dist]

给出多变量符号分布 dist 的 Hoeffding  矩阵.

HoeffdingD[dist,i,j]

对于多变量符号式分布 dist，给出  的第个元素.

更多信息

HoeffdingD[v₁,v₂] 给出了 v₁ 和 v₂ 之间的 Hoeffding 相关性度量 .
Hoeffding  是基于两个列表中的元素相对顺序的相关性度量.
v₁ 和 v₂ 之间的 Hoeffding  由给出，其中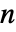是 v₁ 中的观测数目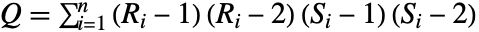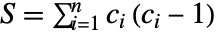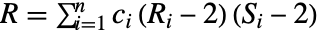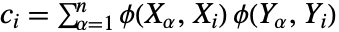，，，，其中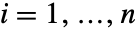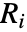，是 v_1i 的秩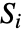，是 v_2i 的秩，而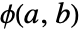等于 Boole[a<b].
参数 v₁ 和 v₂ 可以是长度大于 5 且等长的任意实值向量.
对有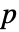列的矩阵 m，HoeffdingD[m] 是由 m 的列之间的相关性度量组成的 × 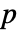的矩阵.
对于 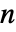× 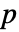的矩阵 m₁ 和 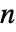× 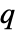的矩阵 m₂，HoeffdingD[m₁,m₂] 是由 m₁ 的列和 m₂ 的列之间的相关性度量组成的 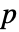× 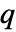的矩阵.
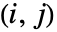
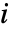HoeffdingD[dist,i,j] 由 30 Expectation[(F[x,y]-G[x]H[y])^2,{x,y}dist_i,j] 给出，其中 F[x,y]、 G[x] 和 H[y] 分别是 dist 的第、第和第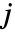个边缘累积分布函数.
HoeffdingD[dist] 给出矩阵 ，其中第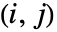个元素由 HoeffdingD[dist,i,j] 给出.

范例

打开所有单元关闭所有单元

基本范例 (4)

两个向量的 Hoeffding ：

矩阵的 Hoeffding ：

两个矩阵的 Hoeffding ：

计算双变量分布的 Hoeffding ：

与模拟数值比较：

范围 (7)

数据 (4)

精确输入产生精确输出：

近似输入产生近似输出：

适用于大型数组：

也可使用 SparseArray 数据：

分布和随机过程 (3)

连续多变量分布的 Hoeffding  矩阵：

导出分布的 Hoeffding  矩阵：

数据分布：

一个随机过程在时刻和的 Hoeffding  矩阵：

应用 (3)

Hoeffding  通常被用于检测非单调依赖结构：

Hoeffding  倾向于对相关向量给出更大的值：

独立向量的值更接近 0：

Hoeffding  可以检测线性相关：

SpearmanRho 和 KendallTau 对线性相关更敏感：

Hoeffding  也可以检测许多类型的非线性相关：

使用 HoeffdingDTest 来确定值是否统计显著：

属性和关系 (4)

Hoeffding  的较大值表明相关性增加：

Hoeffding  矩阵是对称的：

Hoeffding  矩阵的对角元素是 1：

连续双变量分布的 Hoeffding ：

顶部