Insphere

Insphere[{p1,…,pn+1}]

gives the sphere that can be inscribed in the simplex defined by points pi in .

Insphere[poly]

gives the insphere of a polyhedron or polygon poly.

Details

  • Insphere is also known as incircle, inscribed circle, or inscribed disk.
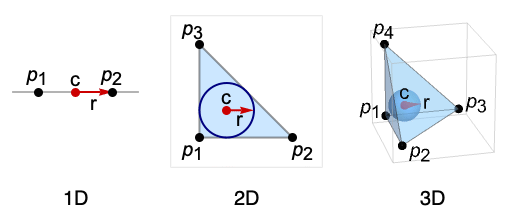
  • Insphere gives the Sphere of largest measure (arc length, area, etc.) that can be inscribed in the simplex (triangle, tetrahedron, etc.) defined by points pi.
  • Insphere evaluates to a Sphere[c,r], where the center c is known as the incenter and radius r is known as the inradius for the related simplex.
  • Insphere is defined for 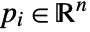and affinely independent.
  • For polyhedra, Insphere[poly] returns a sphere that is contained within the polyhedron poly and tangent to each of the polyhedron faces.
  • For polygons, Insphere[poly] returns a sphere that is contained within the polygon poly and tangent to each of the polygon edges.
  • Insphere can be used with symbolic points in GeometricScene.

Examples

open allclose all

Basic Examples  (2)

An insphere in 2D:

And in 3D:

The insphere of the regular octahedron:

Its surface area:

Scope  (17)

Graphics  (6)

Specification  (2)

Inspheres in different dimensions:

Insphere evaluates to a Sphere:

Get the center and radius:

Styling  (4)

Colored circumspheres:

Different properties can be specified for the front and back of faces using FaceForm:

Inspheres with different specular exponents:

Black circumsphere that glows red:

Opacity specifies the face opacity:

Regions  (11)

Insphere works in any number of dimensions:

Get the circumcenter and circumradius:

Embedding dimension is the dimension of the space in which the sphere lives:

Geometric dimension is the dimension of the shape itself:

Membership testing:

Get conditions for membership:

Area:

Centroid:

Distance from a point:

Plot it:

Signed distance from a point:

Plot it:

Nearest point in the region:

Nearest points to an enclosing sphere:

A sphere is bounded:

Find its range:

Integrate over an Insphere:

Optimize over it:

Solve equations over an Insphere:

Applications  (3)

Recursively construct inscribed triangles and disks:

Use Insphere to generate a circle packing for a triangulated region. First triangulate the region:

Use Insphere to compute a circle for each triangle:

Compute the packing density:

Use Insphere to generate a sphere packing for a triangulated region. First discretize and triangulate the region:

Use Insphere to compute spheres for each tetrahedron:

Compute the packing density:

Properties & Relations  (2)

Insphere is the largest Sphere that can be inscribed in a Simplex:

In 3D:

Use Circumsphere to get a Sphere (blue) that circumscribes a Simplex:

In 3D:

Neat Examples  (1)

Random insphere collections:

Wolfram Research (2015), Insphere, Wolfram Language function, https://reference.wolfram.com/language/ref/Insphere.html (updated 2019).

Text

Wolfram Research (2015), Insphere, Wolfram Language function, https://reference.wolfram.com/language/ref/Insphere.html (updated 2019).

CMS

Wolfram Language. 2015. "Insphere." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Insphere.html.

APA

Wolfram Language. (2015). Insphere. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Insphere.html

BibTeX

@misc{reference.wolfram_2025_insphere, author="Wolfram Research", title="{Insphere}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Insphere.html}", note=[Accessed: 19-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_insphere, organization={Wolfram Research}, title={Insphere}, year={2019}, url={https://reference.wolfram.com/language/ref/Insphere.html}, note=[Accessed: 19-April-2025 ]}