InverseBilateralLaplaceTransform
✖
InverseBilateralLaplaceTransform
詳細とオプション

- 関数
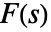 の逆両側ラプラス変換は
の逆両側ラプラス変換は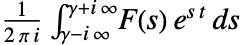 と定義される.ただし,積分は,関数
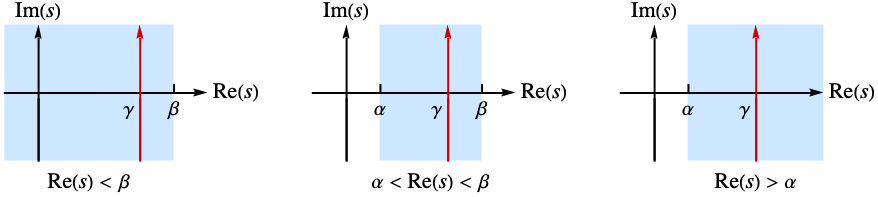
と定義される.ただし,積分は,関数 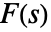 が正則である帯
が正則である帯 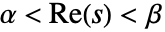 にある垂直線
にある垂直線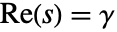 に沿って行われる.場合によっては解析的となる帯が半平面に拡大される.
に沿って行われる.場合によっては解析的となる帯が半平面に拡大される. - 関数
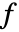 の多次元逆両側ラプラス変換は
の多次元逆両側ラプラス変換は 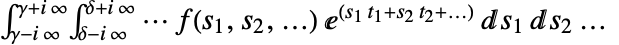 の形の閉曲線積分によって与えられる.
の形の閉曲線積分によって与えられる. - 第3引数
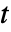 が数値として与えられている場合は,積分が数値メソッドで計算される.
が数値として与えられている場合は,積分が数値メソッドで計算される. - 次は,使用可能なオプションである.
-
AccuracyGoal Automatic 目標とする絶対確度の桁数 Assumptions $Assumptions パラメータについての仮定 GenerateConditions False パラメータについての条件を含む答を生成するかどうか Method Automatic 使用するメソッド PerformanceGoal $PerformanceGoal 最適化しようとするパフォーマンスの局面 PrecisionGoal Automatic 目標とする精度の桁数 WorkingPrecision Automatic 内部計算精度
例題
すべて開くすべて閉じる例 (2)基本的な使用例
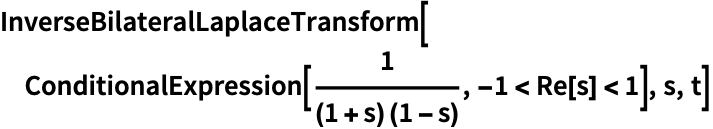
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-g7y74o

https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-usbmnw
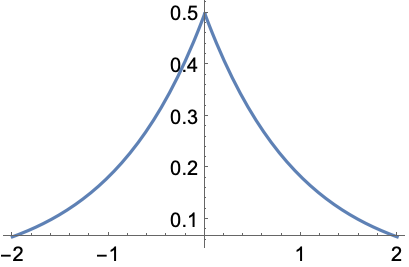
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-34mymg
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-858h6c
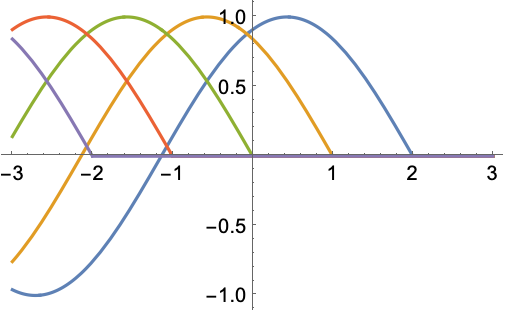
スコープ (13)標準的な使用例のスコープの概要
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-yuu6wa
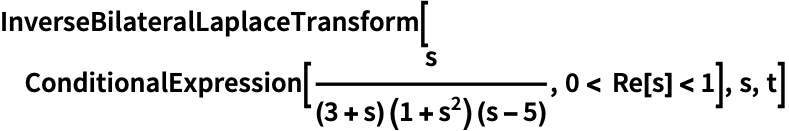
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-3j6aov
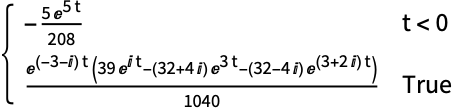
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-y525zg
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-4dys4g
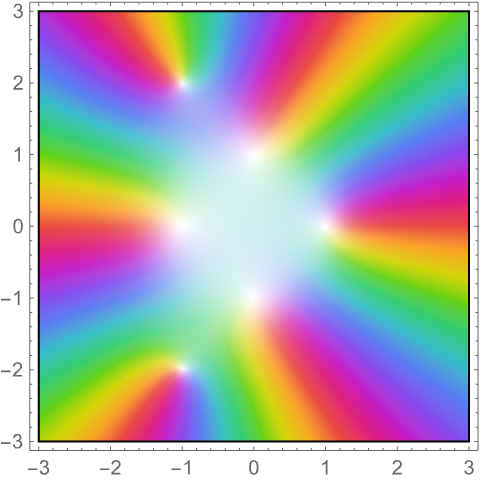
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-1mdbcd
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-7xbzal
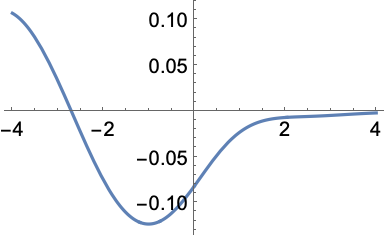
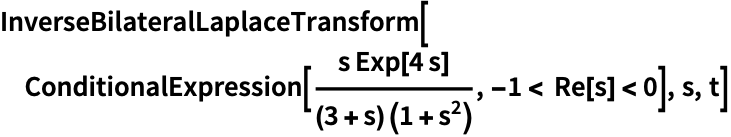
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-6i01lu
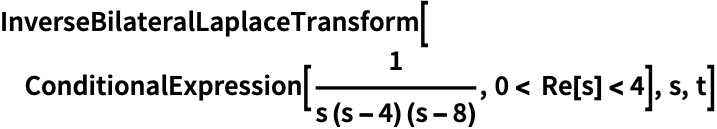
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-505trt
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-lh8c5r
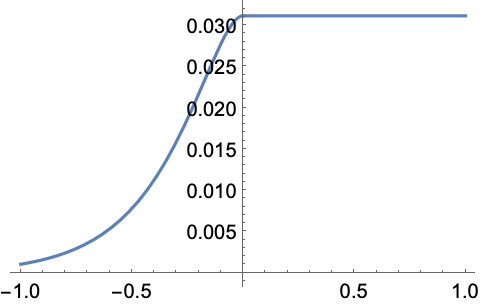
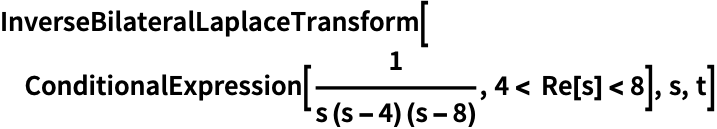
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-2f8cp3
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-te24k8
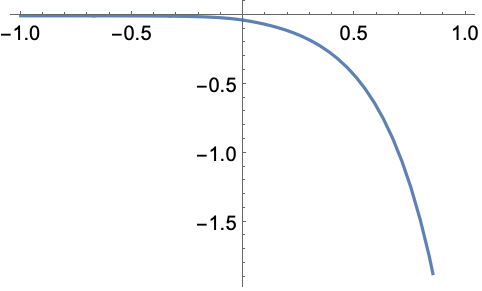
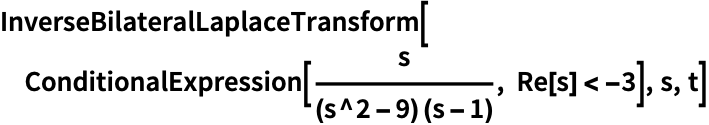
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-74thmm
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-lrtzg6
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-ufywdx
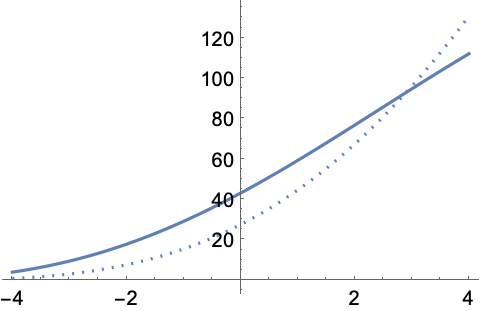
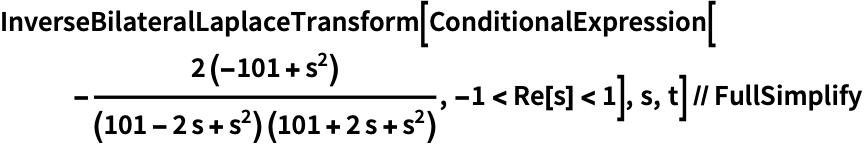
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-8d94wx
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-rrf50t
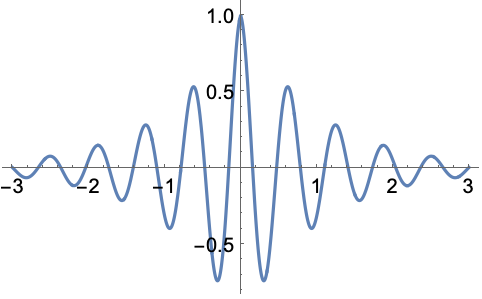
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-gwc85p
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-vozysp
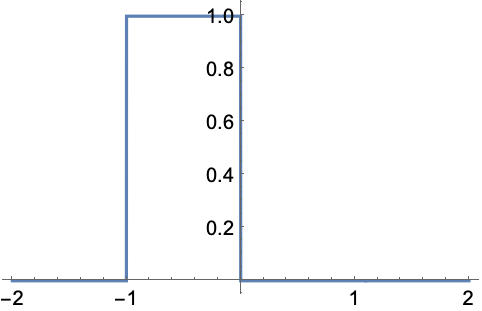
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-pqqn3o
定数の逆両側ラプラス変換はディラック(Dirac)のデルタ関数である:
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-rx21du
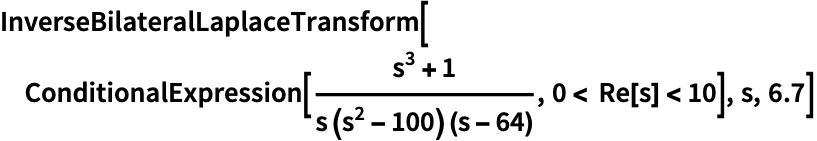
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-kin0zu
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-tu4oar
オプション (3)各オプションの一般的な値と機能
Assumptions (3)
Assumptionsを使ってパラメータの範囲を指定する:
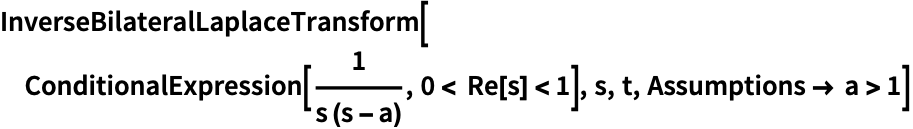
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-xvve2t
Assumptionsを使って極を収束域の外側に置く:
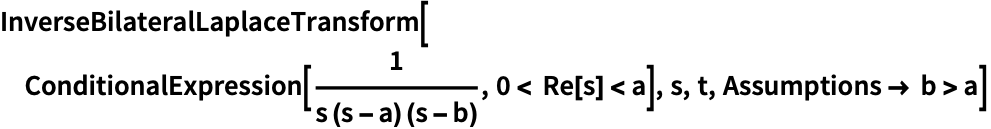
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-neri75
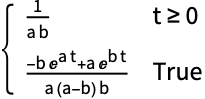
Assumptionsを使って収束域の右端を左半平面に制限する:
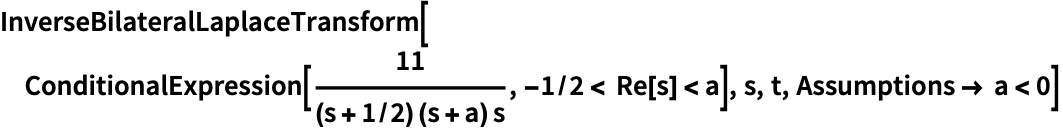
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-jhlsjj
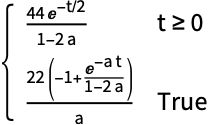
特性と関係 (1)この関数の特性および他の関数との関係
InverseBilateralLaplaceTransformとBilateralLaplaceTransformは互いに互いの逆関数である:
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-si5uys
https://wolfram.com/xid/0ejrhtelmtghotrfpcvbm-f185p5
Wolfram Research (2021), InverseBilateralLaplaceTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.テキスト
Wolfram Research (2021), InverseBilateralLaplaceTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.
Wolfram Research (2021), InverseBilateralLaplaceTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.CMS
Wolfram Language. 2021. "InverseBilateralLaplaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.
Wolfram Language. 2021. "InverseBilateralLaplaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html.APA
Wolfram Language. (2021). InverseBilateralLaplaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html
Wolfram Language. (2021). InverseBilateralLaplaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.htmlBibTeX
@misc{reference.wolfram_2025_inversebilaterallaplacetransform, author="Wolfram Research", title="{InverseBilateralLaplaceTransform}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html}", note=[Accessed: 30-March-2025
]}BibLaTeX
@online{reference.wolfram_2025_inversebilaterallaplacetransform, organization={Wolfram Research}, title={InverseBilateralLaplaceTransform}, year={2021}, url={https://reference.wolfram.com/language/ref/InverseBilateralLaplaceTransform.html}, note=[Accessed: 30-March-2025
]}
