JacobiDN
JacobiDN[u,m]
gives the Jacobi elliptic function ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
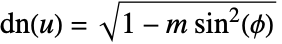 , where
, where 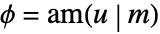 .
. 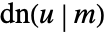 a is doubly periodic function in u with periods
a is doubly periodic function in u with periods 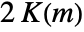 and
and 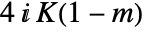 , where
, where 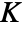 is the elliptic integral EllipticK.
is the elliptic integral EllipticK.- JacobiDN is a meromorphic function in both arguments.
- For certain special arguments, JacobiDN automatically evaluates to exact values.
- JacobiDN can be evaluated to arbitrary numerical precision.
- JacobiDN automatically threads over lists.
Examples
open allclose allBasic Examples (4)
Scope (34)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
Evaluate JacobiDN efficiently at high precision:
Compute average case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix JacobiDN function using MatrixFunction:
Specific Values (3)
Visualization (3)
Function Properties (8)
JacobiDN is ![]() -periodic along the real axis:
-periodic along the real axis:
JacobiDN is ![]() -periodic along the imaginary axis:
-periodic along the imaginary axis:
JacobiDN is an even function in its first argument:
JacobiDN is an analytic function:
It has no singularities or discontinuities:
![]() is neither nondecreasing nor nonincreasing:
is neither nondecreasing nor nonincreasing:
![]() is not injective for any fixed
is not injective for any fixed ![]() :
:
![]() is not surjective for any fixed
is not surjective for any fixed ![]() :
:
In general, it is neither non-negative nor non-positive:
JacobiDN is neither convex nor concave:
Differentiation (3)
Integration (3)
Series Expansions (3)
Plot the first three approximations for ![]() around
around ![]() :
:
Plot the first three approximations for ![]() around
around ![]() :
:
JacobiDN can be applied to a power series:
Function Identities and Simplifications (3)
Parity transformations and periodicity relations are automatically applied:
Identity involving JacobiSN:
Function Representations (3)
Relation to other Jacobi elliptic functions:
TraditionalForm formatting:
Applications (9)
Cartesian coordinates of a pendulum:
Plot the time dependence of the coordinates:
Uniformization of a Fermat cubic ![]() :
:
Conformal map from a unit triangle to the unit disk:
Show points before and after the map:
Check that the solutions fulfill the Nahm equations:
Periodic solution of the nonlinear Schrödinger equation ![]() :
:
Parametrize a lemniscate by arc length [more info]:
Show arc length parametrization and classical parametrization:
Zero modes of the periodic supersymmetric partner potentials:
Complex parametrization of a "sphere":
Plot real and imaginary parts:
Parametrization of a Mylar balloon (two flat sheets of plastic sewn together at their circumference and then inflated):
Properties & Relations (3)
Compose with inverse functions:
Use PowerExpand to disregard multivaluedness of the inverse function:
Evaluate as a result of applying D to JacobiAmplitude:
Text
Wolfram Research (1988), JacobiDN, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiDN.html.
CMS
Wolfram Language. 1988. "JacobiDN." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JacobiDN.html.
APA
Wolfram Language. (1988). JacobiDN. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiDN.html