JacobiSN

JacobiSN[u,m]

gives the Jacobi elliptic function TemplateBox[{u, m}, JacobiSN].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
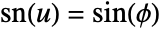  • , where phi=TemplateBox[{u, m}, JacobiAmplitude] and TemplateBox[{u, m}, JacobiAmplitude] is the amplitude.
  • TemplateBox[{u, m}, JacobiSN] is a doubly periodic function in with periods 4 TemplateBox[{m}, EllipticK] and 2 ⅈ TemplateBox[{{1, -, m}}, EllipticK], where 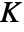is the elliptic integral EllipticK.
  • JacobiSN is a meromorphic function in both arguments.
  • For certain special arguments, JacobiSN automatically evaluates to exact values.
  • JacobiSN can be evaluated to arbitrary numerical precision.
  • JacobiSN automatically threads over lists.

Examples

open allclose all

Basic Examples  (3)

Evaluate numerically:

Series expansions about the origin:

Scope  (34)

Numerical Evaluation  (5)

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Evaluate for complex arguments:

Evaluate JacobiSN efficiently at high precision:

Compute average case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix JacobiSN function using MatrixFunction:

Specific Values  (3)

Simple exact values are generated automatically:

Some poles of JacobiSN:

Find a zero of TemplateBox[{x, {1, /, 3}}, JacobiSN]:

Visualization  (3)

Plot the JacobiSN functions for various values of parameter:

Plot JacobiSN as a function of its parameter :

Plot the real part of TemplateBox[{z, {1, /, 2}}, JacobiSN]:

Plot the imaginary part of TemplateBox[{z, {1, /, 2}}, JacobiSN]:

Function Properties  (8)

JacobiSN is 4 TemplateBox[{m}, EllipticK]-periodic along the real axis:

JacobiSN is 2ⅈTemplateBox[{{1, -, m}}, EllipticK]-periodic along the imaginary axis:

JacobiSN is an odd function in its first argument:

JacobiSN is an analytic function:

It has no singularities or discontinuities:

TemplateBox[{x, {1, /, 3}}, JacobiSN] is neither nondecreasing nor nonincreasing:

TemplateBox[{x, m}, JacobiSN] is not injective for any fixed :

It is injective for :

TemplateBox[{x, m}, JacobiSN] is not surjective for any fixed :

JacobiSN is neither non-negative nor non-positive:

JacobiSN is neither convex nor concave:

Differentiation  (3)

First derivative:

Higher derivatives:

Plot higher derivatives for :

Derivative with respect to :

Integration  (3)

Indefinite integral of JacobiSN:

Definite integral of an odd integrand over the interval centered at the origin is :

More integrals:

Series Expansions  (3)

Taylor expansion for TemplateBox[{x, {1, /, 3}}, JacobiSN]:

Plot the first three approximations for TemplateBox[{x, {1, /, 3}}, JacobiSN] around :

Taylor expansion for TemplateBox[{2, m}, JacobiSN]:

Plot the first three approximations for TemplateBox[{2, m}, JacobiSN] around :

JacobiSN can be applied to power series:

Function Identities and Simplifications  (3)

Parity transformation and periodicity relations are automatically applied:

Automatic argument simplifications:

Identity involving JacobiCN:

Function Representations  (3)

Representation in terms of Sin of JacobiAmplitude:

Relation to other Jacobi elliptic functions:

TraditionalForm formatting:

Applications  (11)

Map a rectangle conformally onto the upper half-plane:

Conformally map a square image onto a disk:

Solution of the pendulum equation:

Check the solution:

Plot solutions:

Cnoidal solution of the Korteweg–De Vries equation:

A numerical check of the solution:

Plot the solution:

Closed form of iterates of the Katsura–Fukuda map:

Compare the closed form with explicit iterations:

Plot a few hundred iterates:

Implicitly defined periodic maximal surface in Minkowski space:

Calculate partial derivatives:

Check numerically the equation for a maximal surface:

Plot the maximal surface in Euclidean space:

Solution of the Euler top equations for :

Check the solutions numerically:

Plot the solutions:

Define a compacton solution of the nonlinear differential equation :

Verify the solution:

Plot the compacton:

The JacobiSN function appears in one of the canonical forms of the Lamé differential equation:

One of the fundamental solutions of this equation is the LameC function:

Solve the Painlevé-VIII differential equation:

Parametrization of a Mylar balloon (two flat sheets of plastic sewn together at their circumference and then inflated):

Properties & Relations  (4)

Compose with inverse functions:

Use PowerExpand to disregard multivaluedness of the inverse function:

Evaluate as a result of applying Sin to JacobiAmplitude:

Solve a transcendental equation:

Numerically find a root of a transcendental equation:

Possible Issues  (2)

Machine-precision input may be insufficient to give the correct answer:

Currently only simple simplification rules are built in for Jacobi functions:

Neat Examples  (1)

Visualize JacobiSN as a function of the parameter in the complex plane:

Wolfram Research (1988), JacobiSN, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiSN.html.

Text

Wolfram Research (1988), JacobiSN, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiSN.html.

CMS

Wolfram Language. 1988. "JacobiSN." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JacobiSN.html.

APA

Wolfram Language. (1988). JacobiSN. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiSN.html

BibTeX

@misc{reference.wolfram_2024_jacobisn, author="Wolfram Research", title="{JacobiSN}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/JacobiSN.html}", note=[Accessed: 26-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_jacobisn, organization={Wolfram Research}, title={JacobiSN}, year={1988}, url={https://reference.wolfram.com/language/ref/JacobiSN.html}, note=[Accessed: 26-December-2024 ]}