DiagonalizableMatrixQ

DiagonalizableMatrixQ[m]

gives True if m is diagonalizable, and False otherwise.

Details and Options

A matrix m is diagonalizable if it is similar to a diagonal matrix. That is, if there is a nonsingular matrix 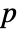such that 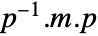is diagonal.
DiagonalizableMatrixQ works for symbolic as well as numerical matrices.
For approximate matrices, the option Tolerance->t can be used to indicate that the determinant of eigenvectors v of the matrix m satisfying Abs[Det[v]]≤t is taken to be zero, which means that the eigenvectors v are linearly dependent and the matrix m is not diagonalizable.
The option Tolerance has Automatic as its default value.

Examples

open allclose all

Basic Examples (2)

Test if a 2×2 numeric matrix is diagonalizable:

Test if a 3×3 symbolic matrix is diagonalizable:

Put the eigenvectors of the matrix in columns:

Verify the matrix is similar to diagonal matrix:

Scope (9)

Basic Uses (5)

Test if a real machine-precision matrix is diagonalizable:

Verify the result:

The diagonal elements of the obtained matrix are the eigenvalues of :

Test if a complex matrix is diagonalizable:

Test if an exact matrix is diagonalizable:

Make the matrix diagonalizable:

Use DiagonalizableMatrixQ with an arbitrary-precision matrix:

A random square matrix is typically diagonalizable:

Use DiagonalizableMatrixQ with a symbolic matrix:

Special Matrices (4)

Use DiagonalizableMatrixQ with sparse matrices:

Use DiagonalizableMatrixQ with structured matrices:

Use with a QuantityArray structured matrix:

The identity matrix is diagonalizable:

HilbertMatrix is diagonalizable:

Options (1)

Tolerance (1)

Generate a real-valued non-diagonalizable Jordan block matrix with some random perturbation of order :

q is diagonalizable:

But the eigenvectors v are numerically linearly dependent:

Adjust the option Tolerance so that the linear dependence of the eigenvectors is detected:

Applications (6)

If a matrix is diagonalizable, it can be decomposed as , where is nonsingular and is diagonal. This can be used to compute a matrix function by using its power series representation as $f(m)=p.(sum_(i=0)^inftya_i d^i).TemplateBox[{p}, Inverse]=p.f(d).TemplateBox[{p}, Inverse]$ , and can be computed by simply applying to each of the diagonal elements. Use this method to compute several different matrix functions:

Compute the eigensystem of :

The matrix has the eigenvectors as columns, and the diagonal entries are the eigenvalues:

Compute and confirm using MatrixPower:

Compute and confirm using MatrixExp:

Compute and confirm using MatrixLog:

Compute and confirm using MatrixFunction:

Solve the system of ODEs , , . First, construct the coefficient matrix for the right-hand side:

The coefficient matrix is diagonalizable, so computing the matrix exponential will be straightforward:

Find the eigenvalues and eigenvectors:

Construct a diagonal matrix whose entries are the exponential of :

Construct the matrix whose columns are the corresponding eigenvectors:

The general solution is , for three arbitrary starting values:

Verify the solution using DSolveValue:

Use the fact that the recurrence relation for Fibonacci, , can be written in matrix form as to derive a formula for the pair . The solution to the recurrence relation is , where :

The matrix is diagonalizable:

Thus, the matrix power can be computed simply using Eigensystem[m]:

Complete the definition of :

Compute and :

Confirm the result using Fibonacci:

Normal matrices are the most general kind of matrix that can be unitarily diagonalized as with diagonal and unitary. All Hermitian matrices are normal because both sides of the equality are simply :

Similarly, all antihermitian matrices are normal because both sides of the equality are simply :

Unitary matrices are normal, as substituting in the definition gives an identity matrix on both sides:

Show that the following matrix is normal, then diagonalize it:

Confirm using NormalMatrixQ:

A normal matrix like can be unitarily diagonalized using Eigensystem:

The entries on the diagonal can be arbitrary complex numbers:

Normalizing the eigenvectors and putting them in columns gives a unitary matrix:

Confirm the diagonalization :

Skipping normalization of the eigenvectors suffices to show that is diagonalizable (though not unitarily):

In quantum mechanics, the energy operator is called the Hamiltonian , and a state with energy evolves according to the Schrödinger equation . An important assumption is that any state can be written as a sum of eigenstates. Show that this is the case for Hamiltonian for a spin-1 particle in constant magnetic field in the direction: