JordanDecomposition

JordanDecomposition[m]

正方行列 m のジョルダン(Jordan)分解を行う．結果として，リスト{s,j}を与える．s は相似行列を表し，j は m のジョルダン標準形を表す．

詳細

  • もとの行列 m は s.j.Inverse[s]に等しい． »
  • 行列 m は数値でも記号でも指定可能である．

例題

すべて開くすべて閉じる

例  (1)

3×3行列のジョルダン分解を求める：

結果をフォーマットする：

スコープ  (10)

基本的な用法  (6)

機械精度行列のジョルダン分解：

結果をフォーマットする：

複素行列のジョルダン分解：

不足固有空間を持つ厳密行列のジョルダン分解：

の第3列の1は，48に対応する固有空間が不足していることを示している：

の第3列は，したがって，がではなく を与える一般化された固有ベクトルである：

任意精度行列のジョルダン分解：

記号行列のジョルダン分解：

大きい数値行列のジョルダン分解は効率的に計算される：

特殊行列  (4)

疎な行列のジョルダン分解：

構造化行列の固有系：

IdentityMatrixはジョルダン標準形である：

関連付けられた類似度行列は恒等行列の平方根である：

HilbertMatrixのジョルダン分解：

アプリケーション  (12)

一般化された固有ベクトルと対角化可能性  (4)

行列 について，ジョルダン分解の 行列の列を真の固有ベクトルと一般化された固有ベクトルの観点から解釈する：

ジョルダン分解を計算する：

対応する （列1, 3, 4）の対角より上にが存在しない の列は，の真の固有ベクトルである：

残りの列はの一般化された固有ベクトルである：

以下の行列には，1つの固有ベクトルしかないがTemplateBox[{}, Reals]^4の基底を形成する一般化された固有ベクトルの完全鎖はあることを示す：

Eigensystemは，84がただ一つの独立固有ベクトルを含む多重度4の固有値であることを示す：

JordanDecompositionの 行列の第1列は固有ベクトルが見付かった列である：

残りの列はである鎖である：

は空のNullSpaceを持つので，その列はTemplateBox[{}, Reals]^4の基底を形成する：

正方行列は固有ベクトルの完全集合を持ち，したがって 行列が対角行列であるときかつそのときに限って対角化可能である：

特定の行列が対角化可能かどうかを調べる：

DiagonalizableMatrixQを使って確かめる：

1と0の4×4行列が対角化可能である確率を推定する：

のとき なら × 行列 はベキ零である：

対角化不可能な行列 について考える：

はJordanDecompositionを使って対角化可能な行列とベキ零行列の和として書くことができる：

が の対角部分と から形成された行列であるとする：

が の上対角部分と から形成された行列であるとする：

そうすると は と の和ということになる：

行列 は対角化可能である：

行列 はベキ零である：

さらに，行列 と行列 は可換である：

対角化  (4)

対角化可能な行列について，ジョルダン分解は対角化を m=s.j.TemplateBox[{s}, Inverse]として直接与える．これを使って行列 を対角化する：

ジョルダン分解を計算する：

対角化を確認する：

は標準行列が行列 で与えられる線形変換であるとする．基底が対角である の表現における特性でTemplateBox[{}, Reals]^4の基底 を求める：

のジョルダン分解を求める：

は固有ベクトルつまり の列からなるとする． が -座標から標準座標に変換されるとその逆行列は逆の方向に変換される：

したがって，は TemplateBox[{s}, Inverse].a.s で与えられるが，これは対角行列である：

これは成分が固有値である単純な対角行列である点に注意のこと：

実数値対称行列 は h=o.d.TemplateBox[{o}, Transpose]として直交対角化可能である．ただし， は実数値の対角で は直交である．以下の行列が対称行列であることを確認してこれを対角化する：

ジョルダン分解を計算する：

が と等しいとする：

列を正規化した後で と が等しいとする：

が実際に直交行列であることを確かめる：

h=o.d.TemplateBox[{o}, Transpose]であることを確認する：

TemplateBox[{n}, ConjugateTranspose].n=n.TemplateBox[{n}, ConjugateTranspose]ならその行列は正規行列と呼ばれる．正規行列はユニタリ変換で対角化可能な最も一般的な行列である．実数値対称行列 は方程式の両辺が単に なのですべて正規行列である：

次の行列が正規行列であることを示し，次にこれを対角化する：

NormalMatrixQを使って確かめる：

ジョルダン分解を計算する：

対角行列は実数値対称行列とは違って複素数値である：

の列を正規化するとユニタリ行列になる：

直交化 n=u.d.TemplateBox[{u}, ConjugateTranspose]を確かめる：

行列関数と動的な系  (4)

以下の行列 についてジョルダン分解を使って とを計算する：

行列と 行列を計算する：

恒等式 m=s.j.TemplateBox[{s}, Inverse]を確認する：

m^k=s.j.TemplateBox[{s}, Inverse].s.j.TemplateBox[{s}, Inverse].....s.j.TemplateBox[{s}, Inverse]=s.j^k.TemplateBox[{s}, Inverse]である． は上三角行列でほぼ対角行列なので，対角成分は 乗され，成分は になる：

したがって，についての式は以下のようになる：

MatrixPowerを使った直接計算で確認する：

指数行列にベキ級数を適用すると，対角成分が明らかにになり，非対角成分は単に指数を再構成した指数和になる．したがって，これもまた になる：

したがって，の式は以下になる：

MatrixExpによる直接計算を使って確かめる：

以下の行列 の単一鎖と ，，の各関数からなるジョルダン行列についての式 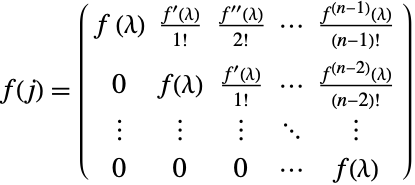を確認する：

まず，についての式を計算する：

MatrixFunctionを使って計算を確かめる：

についての計算も類似している：

MatrixFunctionで結果を確認する：

にはパラメータがあるので，Derivativeの代りにDを使って を代入する：

再度，Functionを使って が入力された際の結果をMatrixFunctionで確認する：

常微分方程式系 , , を解く．まず，右辺についての係数行列 を構築する：

のジョルダン分解を計算する：

前の例の式を使う．は以下で与えられる：

3つの任意の初期値についての一般解はexp(ta).{c_1,c_2,c_3}=s.exp(tj).TemplateBox[{s}, Inverse].{TemplateBox[{1}, CTraditional],TemplateBox[{2}, CTraditional],TemplateBox[{3}, CTraditional]}である：

DSolveValueを使って解を確認する：

動的な系 の一般解を求める．ただし， は以下の確率行列である：

のジョルダン分解を計算する：

は対角行列なので は単に対角成分を 乗したものからなる：

一般解は A^k.{c_1,c_2.c_3}=s.j^k.TemplateBox[{s}, Inverse].{c_1,c_2.c_3}である：

が動的方程式を満足することを確かめる：

特性と関係  (10)

JordanDecomposition[m]は m の行列因子分解を s.j.Inverse[s]として与える：

ジョルダン分解を求める：

m は s.j.Inverse[s]に等しい：

m の固有値は j の対角線上にある：

行列は，そのジョルダン分解の j 行列が対角行列のときかつそのときに限って対角化可能である：

m が対角化可能であれば，ジョルダン分解は実質的にEigensystemと等しい：

要素の順序付けは異なる：

固有値は j の対角上にある：

固有ベクトルは s の列である：

JordanDecompositionは，対角化可能な行列については関数の適用を固有値への適用に限定する：

対角化を使って対角成分のみをベキ乗することで対角化行列指数関数を計算する：

MatrixExpを使って指数行列を計算する：

これは，単に各成分のベキ乗ではない点に注意のこと：

ジョルダン分解は，対角化不可能な行列については関数の適用を一般化された各固有ベクトル鎖への適用に限定する：

j 行列は対角行列ではないので，m は対角化できない：

関数適用は，j が対角より上で1である列については対角の上にしか拡張されない：

f(m)=s.f(j).TemplateBox[{s}, Inverse]であることを確認する：

対称実数値行列について， 行列は直交する：

行列は実数値の対角行列である：

実非対角数値行列については， 行列はユニタリ行列である：

行列は純粋に虚な対角成分を持つ対角行列である：

実ユニタリ数値行列については， 行列はユニタリ行列である：

行列は対角行列である：

対角成分は単位円上にある：

正規数値行列について， 行列はユニタリ行列である：

行列は対角行列である：

数値正規行列 n についてSchurDecomposition[n,RealBlockDiagonalFormFalse]である：

これはジョルダン分解と位相まで一致する：

t 行列と j 行列は等しい：

q が列に固有ベクトルを持つことを確認するために，各列の第1成分を1.に設定して q と s の位相差を消去する：

考えられる問題  (2)

m は，いくつかの成分が多少異なる4×4行列である：

厳密演算でジョルダン分解を求める：

次は，m が対角化可能であることを示す：

機械数演算でジョルダン分解を求める：

機械数による演算での計算は，行列が対角化可能ではないことを示唆している：

機械精度にすると，m は近傍の対角化不可能な行列と区別できない：

行列 m にはいくつかの機械精度の成分がある：

数値丸のために2.における欠損固有空間は別々の2つの固有区間に分離される：

厳密演算で計算して行列が対角化可能かどうかを判定する：

Wolfram Research (1996), JordanDecomposition, Wolfram言語関数， https://reference.wolfram.com/language/ref/JordanDecomposition.html （2010年に更新）.

テキスト

Wolfram Research (1996), JordanDecomposition, Wolfram言語関数， https://reference.wolfram.com/language/ref/JordanDecomposition.html （2010年に更新）.

CMS

Wolfram Language. 1996. "JordanDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/JordanDecomposition.html.

APA

Wolfram Language. (1996). JordanDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JordanDecomposition.html

BibTeX

@misc{reference.wolfram_2024_jordandecomposition, author="Wolfram Research", title="{JordanDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanDecomposition.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_jordandecomposition, organization={Wolfram Research}, title={JordanDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanDecomposition.html}, note=[Accessed: 22-November-2024 ]}