WOLFRAM

Wolfram 语言与系统 参考资料中心
Wolfram 语言首页 »

JordanDecomposition
✖
JordanDecomposition

✖

产生一个方阵 m 的 Jordan 分解. 结果是一个列表 {s,j}，其中 s 是一个相似矩阵，j 是 m 的 Jordan 范式.

更多信息

  • 原矩阵 m 等于 s.j.Inverse[s]. »
  • 矩阵 m 是数值型或者是符号型.

范例

打开所有单元关闭所有单元

基本范例  (1)常见实例总结

出 3×3 矩阵的 Jordan 分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-cu62lx
Out[1]=1

格式化结果：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-dn6gpb
Out[2]=2

范围  (10)标准用法实例范围调查

基本用法  (6)

机器精度矩阵的约旦分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-zu0gyk
Out[1]=1

格式化结果：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-h1ahoy
Out[2]=2

复矩阵的约旦分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-zrmlpw
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-7iibn6
Out[2]=2

具有亏特征空间 (deficient eigenspace) 的精确矩阵的约旦分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-vyrris
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-f1rxq4
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-i9tzbx
Out[3]=3

的第三列中的 1 表明对应于 48 的特征空间是亏的：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-n6ilek
Out[4]=4

因此 的第三列是一个广义的特征向量，其中 给出 ，而不是 ：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-n5y3nu
Out[5]=5

任意精度矩阵的约旦分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-fdp2bk
Out[1]=1

符号矩阵的约旦分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-kh8lz1
Out[1]=1

高效计算大型数值矩阵的约旦分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-madl2m
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-0ipkhx
Out[2]=2

特殊矩阵  (4)

稀疏矩阵的约旦分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-g3c1vo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-6pl8u9
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-wrpyns
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-30cyz3
Out[4]=4

结构化矩阵的特征系统：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-k0xjhe
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-pthoj7
Out[2]=2

IdentityMatrix 是约旦标准型：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-4x01lt
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-oy5mpe
Out[2]=2

关联的相似矩阵是单位矩阵的平方根：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-frdsxs
In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-f63083
Out[4]=4

HilbertMatrix 的约旦分解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-mqxkx3
Out[1]=1

应用  (12)用该函数可以解决的问题范例

广义特征向量和可对角化性  (4)

对于矩阵 ，根据真实特征向量和广义特征向量解释约旦分解的 矩阵的列：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-6gbrq4

计算约旦分解：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-gfzptm
Out[3]=3

在对应的 — 第 1、3 和 4 列— 的对角线上没有 的 的列是真正的特征向量，其中 ：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-i7a8ov
Out[4]=4

剩余的列是一个广义特征向量，其中 ：

In[9]:=9
✖
https://wolfram.com/xid/0b0mapsa4pe-6evvit
Out[9]=9

证明下面的矩阵只有一个特征向量，但它有一个完整的广义特征向量链，构成了 TemplateBox[{}, Reals]^4 的基：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-odtwt9

Eigensystem 显示 84 是重数为 4 的特征值，它只有一个独立的特征向量：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-dnjjd3
Out[2]=2

JordanDecomposition 的 矩阵的第一列是找到的一个特征向量：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-bwrb23
Out[3]=3

其余的列是一个链，其中 ：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-qc1zvl
Out[4]=4

由于 的 NullSpace 为空，其列构成 TemplateBox[{}, Reals]^4 的基：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-hkktev
Out[5]=5

有且仅有当方块矩阵的 矩阵为对角矩阵时，其有完整的特征向量组，因此该矩阵可对角化：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-h6peol

测试特定矩形是否对角化：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-16pr0x
Out[2]=2

使用 DiagonalizableMatrixQ 进行验证：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-70uv9z
Out[3]=3

估计一个由 1 和 0 组成的 4×4 矩阵对角化的概率：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-oykxfq
Out[4]=4

对于 ，如果 ，则一个 × 的矩阵 是幂零矩阵：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-7q1re9
Out[1]=1

考虑不可对角化的矩阵 ：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-vxl6ny
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-s3q83e
Out[3]=3

可用 JordanDecomposition 将 写成可对角化矩阵和幂零矩阵的和：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-jpeinx
Out[4]=4

令 为 和 的对角部分形成的矩阵：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-wf0ucl
Out[5]=5

令 为 和 的超对角部分形成的矩阵：

In[6]:=6
✖
https://wolfram.com/xid/0b0mapsa4pe-kcsi17
Out[6]=6

则 i是 和 的和：

In[7]:=7
✖
https://wolfram.com/xid/0b0mapsa4pe-qgcrxh
Out[7]=7

矩阵 是可对角化的：

In[8]:=8
✖
https://wolfram.com/xid/0b0mapsa4pe-us5pk1
Out[8]=8

矩阵 是幂零矩阵：

In[9]:=9
✖
https://wolfram.com/xid/0b0mapsa4pe-0a8wrj
Out[9]=9

而且，矩阵 和 是可交换的：

In[10]:=10
✖
https://wolfram.com/xid/0b0mapsa4pe-fpmzz2
Out[10]=10

对角化  (4)

对于可对角化矩阵，约旦分解直接给出其对角化为 m=s.j.TemplateBox[{s}, Inverse]. 将其应用于将矩阵 对角化：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-7gdki7

计算约旦分解：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-q713gz
Out[3]=3

验证对角化：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-jt277v
Out[4]=4

令 为线性变换，其标准矩阵由矩阵 给出. 求得 TemplateBox[{}, Reals]^4 的基 ，在该基 中 表示的属性为对角矩阵：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-hld5cy

求 的约旦分解：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-o61dga
Out[2]=2

令 由特征向量组成，即 的列. 当 从 坐标转换为标准坐标时，其逆向转换为相反方向：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-6tp8ia
Out[3]=3

因此 TemplateBox[{s}, Inverse].a.s 给出 ，且为对角矩阵：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-gefesr

请注意，这只是对角矩阵，其项是特征值：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-ytgfvr
Out[5]=5

实值对称矩阵 可正交对角化为 h=o.d.TemplateBox[{o}, Transpose]，其中 为实值对角矩阵且 为正交. 验证以下矩阵是对称的，然后对其进行对角化：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-t0tayn
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-d26vmx
Out[2]=2

计算约旦分解：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-mbie39

令 等于 ：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-c0pq92

令 在正规化其列后等于 ：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-2tw7d1

验证 实际上为正交矩阵：

In[6]:=6
✖
https://wolfram.com/xid/0b0mapsa4pe-cuel5e
Out[6]=6

验证 h=o.d.TemplateBox[{o}, Transpose]：

In[7]:=7
✖
https://wolfram.com/xid/0b0mapsa4pe-4fffl2
Out[7]=7

若 TemplateBox[{n}, ConjugateTranspose].n=n.TemplateBox[{n}, ConjugateTranspose] 则矩阵被称为正规矩阵. 正规矩阵是最通用的一种矩阵，可以通过酉变换对角化. 所有实对称矩阵 都是正规矩阵，因为等式的两边都是 ：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-6b09sy
Out[1]=1

证明下面的矩阵是正规的，并对其进行对角化：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-exqe2b
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-wqtvhs
Out[3]=3

使用 NormalMatrixQ 验证：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-46r3j6
Out[4]=4

计算约旦分解：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-0bbmuk

不像实对称矩阵，该对角矩阵的值为复数：

In[6]:=6
✖
https://wolfram.com/xid/0b0mapsa4pe-8d13py

对 的列进行正规化得到酉矩阵：

In[7]:=7
✖
https://wolfram.com/xid/0b0mapsa4pe-3xuanx
In[8]:=8
✖
https://wolfram.com/xid/0b0mapsa4pe-64w99o
Out[8]=8

验证对角化 n=u.d.TemplateBox[{u}, ConjugateTranspose]：

In[9]:=9
✖
https://wolfram.com/xid/0b0mapsa4pe-2hpiyq
Out[9]=9

矩阵函数和动态系统  (4)

使用约旦分解计算下列矩阵 的 话 ：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-jqh2nk

计算 和 矩阵：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-lo6s0e
Out[3]=3

验证单位矩阵 m=s.j.TemplateBox[{s}, Inverse]：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-x8d19i
Out[4]=4

然后 m^k=s.j.TemplateBox[{s}, Inverse].s.j.TemplateBox[{s}, Inverse].....s.j.TemplateBox[{s}, Inverse]=s.j^k.TemplateBox[{s}, Inverse]. 由于 是上三角形且接近对角线，因此对角线项的乘方为 ，项 变为 ：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-2mtd8o

因此 的表达式为：

In[6]:=6
✖
https://wolfram.com/xid/0b0mapsa4pe-1ms4pa

通过 MatrixPower 的直接计算进行验证：

In[7]:=7
✖
https://wolfram.com/xid/0b0mapsa4pe-ut4jb3
Out[7]=7

应用指数的幂级数，对角线项变成 ，而非对角线项只是重新索引的指数和. 因此，它也变成了 ：

In[8]:=8
✖
https://wolfram.com/xid/0b0mapsa4pe-x4ujj6

因此 的表达式为：

In[9]:=9
✖
https://wolfram.com/xid/0b0mapsa4pe-v3k1is

通过 MatrixExp 的计算进行验证：

In[10]:=10
✖
https://wolfram.com/xid/0b0mapsa4pe-3chst3
Out[10]=10

验证约旦矩阵的方程 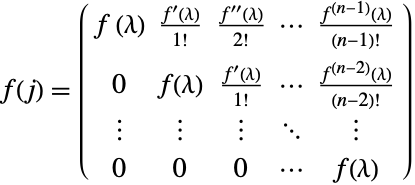，该约旦矩阵由下列矩阵 和函数 , 和 的单链组成：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-qbmjxa

首先计算 的方程：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-p6jlws

使用 MatrixFunction 验证该计算：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-405v2o
Out[3]=3

的计算也类似：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-pb24s4

MatrixFunction 验证了该结果：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-v2l3rx
Out[5]=5

由于 有参数，需要使用 D 而非 Derivative，并在 中代换：

In[6]:=6
✖
https://wolfram.com/xid/0b0mapsa4pe-x8nm0q

同样，当使用 Function 输入 时，MatrixFunction 确认结果：

In[7]:=7
✖
https://wolfram.com/xid/0b0mapsa4pe-j6f7ys
Out[7]=7

求解常微分方程组 , , . 首先，构建右侧的系数矩阵 ：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-uoeghr

计算 的约旦分解：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-7s4qu6
Out[2]=2

使用前面例子的方程式， 由下式给出：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-p91gkv

通解为 exp(ta).{c_1,c_2,c_3}=s.exp(tj).TemplateBox[{s}, Inverse].{TemplateBox[{1}, CTraditional],TemplateBox[{2}, CTraditional],TemplateBox[{3}, CTraditional]}，对于三个任意的起始值：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-flftlr

使用 DSolveValue 验证解：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-neb1o5
Out[5]=5

当 是以下随机矩阵时，生成动态系统 的一般解：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-pp2m0k

计算 的约旦分解：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-hcmla7
Out[2]=2

由于 为对角矩阵， 仅包括对角项的 次幂：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-q30bvq
Out[3]=3

通解为 A^k.{c_1,c_2.c_3}=s.j^k.TemplateBox[{s}, Inverse].{c_1,c_2.c_3}：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-ow6p6z
Out[4]=4

验证 满足动态方程：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-7yd97k
Out[5]=5

属性和关系  (10)函数的属性及与其他函数的关联

JordanDecomposition[m] 给出 m 的矩阵分解为 s.j.Inverse[s]：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-nkzr7p

求 Jordan 分解：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-qkayu8
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-eu2pjn
Out[3]=3

m 等于 s.j.Inverse[s]：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-jm2k7d
Out[4]=4

m 特征值是 j 的对角元素：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-fulz9x
Out[5]=5

当且仅当约旦分解的 j 矩阵为对角矩阵，该矩阵可对角化：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-4mwr0y
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-5dg1a0
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-1vzwst
In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-wt6fit
Out[4]=4

如果 m 是对角化的，Jordan 分解实际上和 Eigensystem 相同：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-gk9m34
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-3asj2m
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-ll6wi1
Out[3]=3

次序是不相同：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-onu3q4
Out[4]=4

特征值是 j 的对角元素：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-k3rk6n
Out[5]=5

特征向量是 s 的列元素：

In[6]:=6
✖
https://wolfram.com/xid/0b0mapsa4pe-flnp05
Out[6]=6

对于可对角化矩阵， JordanDecomposition 将函数应用简化为特征值的应用：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-6ufrqm

使用对角化计算矩阵指数，仅对对角线项求幂：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-tlnt0f
Out[2]=2

使用 MatrixExp 计算矩阵指数：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-c6fiyq
Out[3]=3

请注意，这不仅仅是每个项的指数：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-y2pltu
Out[4]=4

对于不可对角化矩阵，约旦分解将函数应用限制在每个广义特征向量链上：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-kt5xge
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-wcrgtj

j 矩阵不是对角矩阵，所以 m 不可对角化：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-qwbsg3

对于 j 在对角线上方有 1 的列，函数应用仅扩展到对角线上方：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-e2owjo

验证 f(m)=s.f(j).TemplateBox[{s}, Inverse]：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-hfvq78
Out[5]=5

对于实对称数值矩阵， 矩阵是正交矩阵：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-40f8st
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-zw892l
Out[2]=2

矩阵为对角实数矩阵：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-1n3v4a
Out[3]=3

对于实反对称数值矩阵， 矩阵是酉矩阵：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-2d2hq1
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-xvt54m
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-nm40tw
Out[3]=3

矩阵是有纯虚对角项的对角矩阵：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-wwepwu
Out[4]=4

对于实酉数值矩阵， 矩阵是酉矩阵：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-4w1n61
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-3y0ct4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-mclbfd
Out[3]=3

矩阵为对角矩阵：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-wz0l89
Out[4]=4

对角线项位于单位圆上：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-jxr4wq
Out[5]=5

对于正规数值矩阵， 矩阵是酉矩阵：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-45k79q
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-mylxd7
Out[2]=2

矩阵为对角矩阵：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-c1kzdd
Out[3]=3

正规矩阵 n 的 SchurDecomposition[n,RealBlockDiagonalFormFalse]：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-df3aev
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-r3cio0
Out[2]=2

到这里，结果与约旦分解一致：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-j7q4dl
Out[3]=3

t 和 j 矩阵相等：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-3ehy88
Out[4]=4

为验证 q 是否具有特征向量作为列，将每列的第一个条目设置为 1. 可以消除 q 和 s 之间的相位差：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-jkbsky
Out[5]=5

可能存在的问题  (2)常见隐患和异常行为

m 是一个 4×4 矩阵，其中一些项略有不同：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-ph4cew

用明确算法求 Jordan 分解：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-lct9tf

这显示 m 是对角化的：

In[5]:=5
✖
https://wolfram.com/xid/0b0mapsa4pe-qcoehp
Out[5]=5

用机器数算法求 Jordan 分解：

In[4]:=4
✖
https://wolfram.com/xid/0b0mapsa4pe-ecnkgj
Out[4]=4

用机器数算法的计算来指定矩阵不是对角化的：

In[6]:=6
✖
https://wolfram.com/xid/0b0mapsa4pe-3csgas
Out[6]=6

对于机器精度，m 是难区分非对角矩阵的形式：

In[7]:=7
✖
https://wolfram.com/xid/0b0mapsa4pe-bxlmii
Out[7]=7

矩阵 m 有一些机器精度的项：

In[1]:=1
✖
https://wolfram.com/xid/0b0mapsa4pe-jsnhn2

由于数值四舍五入，2. 处的缺陷特征空间被分成两个独立的特征空间：

In[2]:=2
✖
https://wolfram.com/xid/0b0mapsa4pe-41jhie

使用精确算术进行计算，确定矩阵是否可对角化：

In[3]:=3
✖
https://wolfram.com/xid/0b0mapsa4pe-prbuv6
Wolfram Research (1996)，JordanDecomposition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JordanDecomposition.html （更新于 2010 年）.
✖
Wolfram Research (1996)，JordanDecomposition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JordanDecomposition.html （更新于 2010 年）.

文本

Wolfram Research (1996)，JordanDecomposition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JordanDecomposition.html （更新于 2010 年）.

✖
Wolfram Research (1996)，JordanDecomposition，Wolfram 语言函数，https://reference.wolfram.com/language/ref/JordanDecomposition.html （更新于 2010 年）.

CMS

Wolfram 语言. 1996. "JordanDecomposition." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2010. https://reference.wolfram.com/language/ref/JordanDecomposition.html.

✖
Wolfram 语言. 1996. "JordanDecomposition." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2010. https://reference.wolfram.com/language/ref/JordanDecomposition.html.

APA

Wolfram 语言. (1996). JordanDecomposition. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/JordanDecomposition.html 年

✖
Wolfram 语言. (1996). JordanDecomposition. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/JordanDecomposition.html 年

BibTeX

@misc{reference.wolfram_2025_jordandecomposition, author="Wolfram Research", title="{JordanDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanDecomposition.html}", note=[Accessed: 02-April-2025 ]}

✖
@misc{reference.wolfram_2025_jordandecomposition, author="Wolfram Research", title="{JordanDecomposition}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JordanDecomposition.html}", note=[Accessed: 02-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_jordandecomposition, organization={Wolfram Research}, title={JordanDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanDecomposition.html}, note=[Accessed: 02-April-2025 ]}

✖
@online{reference.wolfram_2025_jordandecomposition, organization={Wolfram Research}, title={JordanDecomposition}, year={2010}, url={https://reference.wolfram.com/language/ref/JordanDecomposition.html}, note=[Accessed: 02-April-2025 ]}