KendallTau
KendallTau[v1,v2]
ベクトル v1と v2についてのケンドール(Kendall)の順位相関係数 ![]() を与える.
を与える.
KendallTau[m]
行列 m についてのケンドールの順位相関係数 ![]() を与える.
を与える.
KendallTau[m1,m2]
行列 m1と m2 についてのケンドールの順位相関係数 ![]() を与える.
を与える.
KendallTau[dist]
多変量記号分布 dist についてのケンドールの順位相関行列を与える.
KendallTau[dist,i,j]
多変量記号分布 dist についてのケンドールの第![]()
![]() 番目の順位相関を与える.
番目の順位相関を与える.
詳細

- KendallTau[v1,v2]は,v1と v2の間のケンドールの順位相関係数
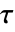 を与える.
を与える. - ケンドールの
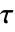 は,2つのリストの連続する要素の相対順位に基づく単調関係の尺度である.
は,2つのリストの連続する要素の相対順位に基づく単調関係の尺度である. 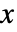 と
と 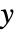 の間のケンドールの
の間のケンドールの 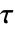 は
は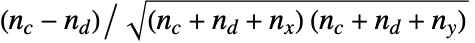 で与えられる.ただし,
で与えられる.ただし,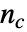 は観測で一致するペアの数,
は観測で一致するペアの数,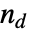 は一致しないペアの数,
は一致しないペアの数,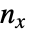 は
は 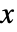 変数のみを含むタイの数,
変数のみを含むタイの数,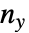 は
は 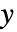 変数のみを含むタイの数である.
変数のみを含むタイの数である.- 観測
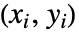 と
と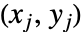 の一致するペアとは,
の一致するペアとは,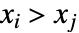 かつ
かつ 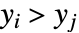 または
または 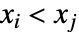 かつ
かつ 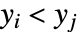 であるもののことである.観測の一致しないペアとは,
であるもののことである.観測の一致しないペアとは,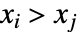 かつ
かつ 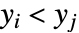 または
または 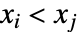 かつ
かつ 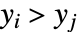 であるもののことである.
であるもののことである. - ケンドールの
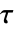 が返したものにタイ修正を施したものはケンドールの
が返したものにタイ修正を施したものはケンドールの 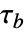 すなわちタウbと呼ばれることがある.
すなわちタウbと呼ばれることがある. - 引数 v1と v2 は任意の同じ長さの実ベクトルでよい.
- 列数が
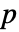 の行列 m について,KendallTau[m]は,m の列間に順位相関がある
の行列 m について,KendallTau[m]は,m の列間に順位相関がある 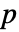 ×
×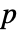 行列である.
行列である. 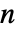 ×
×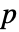 行列 m1と
行列 m1と 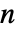 ×
×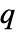 行列 m2については,KendallTau[m1,m2]は m1の列と m2の列の間に順位相関がある
行列 m2については,KendallTau[m1,m2]は m1の列と m2の列の間に順位相関がある 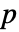 ×
×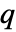 行列である.
行列である.- KendallTau[dist,i,j]は一致の確率から不一致の確率を引いたもの,Probability[(x1-x2)(y1-y2)>0,{{x1,y1}disti,j,{x2,y2}disti,j}]-Probability[(x1-x2)(y1-y2)<0,{{x1,y1}disti,j,{x2,y2}disti,j}]である.ただし,disti,j は dist の第
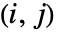 周辺分布である.
周辺分布である. - KendallTau[dist]は第
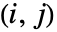
 要素がKendallTau[dist,i,j]で与えられる
要素がKendallTau[dist,i,j]で与えられる 行列
行列 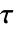 を与える.
を与える.
例題
すべて開くすべて閉じる例 (4)
スコープ (7)
データ (4)
アプリケーション (4)
ケンドールの ![]() は,一般に2つのベクトル間の線形従属性を検出するために使われる:
は,一般に2つのベクトル間の線形従属性を検出するために使われる:
強い線形従属性がある場合,![]() の絶対的な大きさは1に近くなる:
の絶対的な大きさは1に近くなる:
HoeffdingDを使って,その他の依存構造を検出することができる:
ボストン郊外の506の地区で,さまざまな因子が住宅価格にどのような影響を与えているのかを調査するために一連の因子の測定が行われた.酸化窒素濃度と住宅価格の中央値等の因子間の有意な相関は,相関が必ずしも因果関係を含意しないことを思い起こさせるものである:
小売り以外の商業施設の割合,酸化窒素濃度,住宅価格の中央値を比較する散布図の行列:
KendallTauTestは酸化窒素濃度が高くなると住宅価格が下落することを示唆している:
特性と関係 (8)
ケンドールの ![]() の範囲は,高い否定的関連性を示す-1から高い関連性を示す1までである:
の範囲は,高い否定的関連性を示す-1から高い関連性を示す1までである:
ケンドールの ![]() はSpearmanRhoに関連している:
はSpearmanRhoに関連している:
弱線形関係があるとき,SpearmanRhoは![]()
![]() に近くなる:
に近くなる:
KendallTauTestを使って独立性の検定を行う:
あるいは,IndependenceTestを使って適切な検定を自動的に選ぶ:
ケンドールの ![]() は,変数が完全に単調で関係しているときは1または-1になる:
は,変数が完全に単調で関係しているときは1または-1になる:
これは線形関係を厳密に測るCorrelationとは対照的である:
テキスト
Wolfram Research (2012), KendallTau, Wolfram言語関数, https://reference.wolfram.com/language/ref/KendallTau.html.
CMS
Wolfram Language. 2012. "KendallTau." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KendallTau.html.
APA
Wolfram Language. (2012). KendallTau. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KendallTau.html