KendallTau[v1,v2]
对于向量 v1 和 v2,给出 Kendall 的阶数相关性系数 ![]() .
.
KendallTau[m]
对于矩阵 m,给出 Kendall 的阶数相关性系数 ![]() .
.
KendallTau[m1,m2]
对于矩阵 m1 和 m2,给出 Kendall 的阶数相关性系数 ![]() .
.
KendallTau[dist]
对于多变量符号式分布 dist,给出 Kendall 的阶数相关性矩阵.
KendallTau[dist,i,j]
对于多变量符号式分布 dist,给出第 ![]() Kendall 阶数相关性.
Kendall 阶数相关性.


KendallTau
KendallTau[v1,v2]
对于向量 v1 和 v2,给出 Kendall 的阶数相关性系数 ![]() .
.
KendallTau[m]
对于矩阵 m,给出 Kendall 的阶数相关性系数 ![]() .
.
KendallTau[m1,m2]
对于矩阵 m1 和 m2,给出 Kendall 的阶数相关性系数 ![]() .
.
KendallTau[dist]
对于多变量符号式分布 dist,给出 Kendall 的阶数相关性矩阵.
KendallTau[dist,i,j]
对于多变量符号式分布 dist,给出第 ![]() Kendall 阶数相关性.
Kendall 阶数相关性.
更多信息

- KendallTau[v1,v2] 给出位于 v1 和 v2 之间的 Kendall 的阶数相关性系数
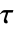 .
. - Kendall 的
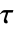 是基于两个列表的连续元素的相对顺序的单调关联性测量.
是基于两个列表的连续元素的相对顺序的单调关联性测量. - 位于
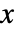 和
和 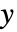 之间的 Kendall 的
之间的 Kendall 的 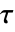 由
由 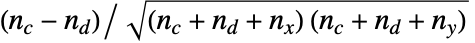 给出,其中
给出,其中 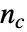 是一致的观测数对,
是一致的观测数对, 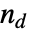 是不一致的对的数目,
是不一致的对的数目,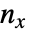 是只涉及
是只涉及 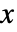 变量的等值数目,而
变量的等值数目,而 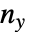 是只涉及
是只涉及 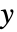 变量的等值数目.
变量的等值数目. - 一致的观测数对
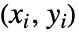 和
和 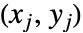 同时满足
同时满足 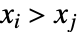 和
和 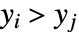 或者同时满足
或者同时满足 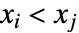 和
和 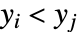 . 不一致的观测数对同时满足
. 不一致的观测数对同时满足 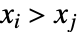 和
和 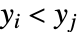 或者同时满足
或者同时满足 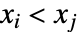 和
和 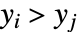 .
. - 返回的 Kendall 的
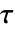 的等值校验版本有时候称为 Kendall
的等值校验版本有时候称为 Kendall 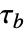 的 Tau-b.
的 Tau-b. - 参数 v1 和 v2 可以是相等长度的任意实值向量.
- 对于具有
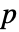 列的矩阵 m,KendallTau[m] 是由位于 m 的列之间的阶数相关性组成的
列的矩阵 m,KendallTau[m] 是由位于 m 的列之间的阶数相关性组成的 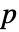 ×
×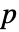 矩阵.
矩阵. - 对于
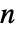 ×
×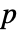 矩阵 m1 和
矩阵 m1 和 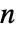 ×
×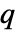 矩阵 m2,KendallTau[m1,m2] 是由位于 m1 的列之间和 m2 的列之间的阶数相关性组成的
矩阵 m2,KendallTau[m1,m2] 是由位于 m1 的列之间和 m2 的列之间的阶数相关性组成的 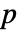 ×
×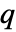 矩阵.
矩阵. - KendallTau[dist,i,j] 是一致概率减去偏差概率 Probability[(x1-x2)(y1-y2)>0,{{x1,y1}disti,j,{x2,y2}disti,j}]-Probability[(x1-x2)(y1-y2)<0,{{x1,y1}disti,j,{x2,y2}disti,j}] 其中 disti,j 是 dist 的第
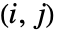 边缘分布.
边缘分布. - KendallTau[dist] 给出矩阵
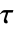 ,其中第
,其中第 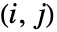 元素是由 KendallTau[dist,i,j] 给出的.
元素是由 KendallTau[dist,i,j] 给出的.
范例
打开所有单元 关闭所有单元范围 (7)
数据 (4)
应用 (4)
HoeffdingD 可用于检测其他独立性结构:
在 506 个波士顿郊区测量一系列因子,确定这些因素与房屋价值的相关性. 例如氮氧化物浓度和房屋价值中位数之类的因素之间的强关联表明相关性并不意味着因果关系:
散点图矩阵比较非零售业务、氮氧化物浓度、房屋价值中位数的比例:
KendallTauTest 说明氮氧化物的浓度增加时,房屋价值下降:
属性和关系 (8)
对于高负相关和高正相关,Kendall 的 ![]() 范围分别为 -1 到 1:
范围分别为 -1 到 1:
Kendall 的 ![]() 与 SpearmanRho 相关:
与 SpearmanRho 相关:
给定弱线性相关,SpearmanRho 大约趋向于 ![]()
![]() :
:
使用 KendallTauTest 来测试独立性:
或者,使用 IndependenceTest 来自动选择适当的测试方法:
如果变量很好地单调相关,Kendall 的 ![]() 将保持 1 或者 -1:
将保持 1 或者 -1:
与 Correlation 相反,它严格测量线性相关性:
文本
Wolfram Research (2012),KendallTau,Wolfram 语言函数,https://reference.wolfram.com/language/ref/KendallTau.html.
CMS
Wolfram 语言. 2012. "KendallTau." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/KendallTau.html.
APA
Wolfram 语言. (2012). KendallTau. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/KendallTau.html 年
BibTeX
@misc{reference.wolfram_2025_kendalltau, author="Wolfram Research", title="{KendallTau}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/KendallTau.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_kendalltau, organization={Wolfram Research}, title={KendallTau}, year={2012}, url={https://reference.wolfram.com/language/ref/KendallTau.html}, note=[Accessed: 03-March-2026]}