LameS
LameS[ν,j,z,m]
gives the ![]()
![]() Lamé function
Lamé function ![]() of order
of order ![]() with elliptic parameter
with elliptic parameter ![]() .
.
Details

- LameS belongs to the Lamé class of functions and solves boundary-value problems for Laplace's equation in ellipsoidal and spheroconal coordinates, as well as occurring in other problems of mathematical physics and quantum mechanics.
- Mathematical function, suitable for both symbolic and numerical manipulation.
- LameS[ν,j,z,m] satisfies the Lamé differential equation
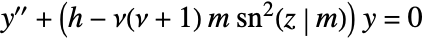 , with the Lamé eigenvalue
, with the Lamé eigenvalue 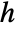 given by LameEigenvalueB[ν,j,m], and where
given by LameEigenvalueB[ν,j,m], and where ![TemplateBox[{z, m}, JacobiSN] TemplateBox[{z, m}, JacobiSN]](Files/LameS.en/8.png) is the Jacobi elliptic function JacobiSN[z,m].
is the Jacobi elliptic function JacobiSN[z,m]. - For certain special arguments, LameS automatically evaluates to exact values.
- LameS can be evaluated to arbitrary numerical precision for arbitrary complex argument.
- LameS automatically threads over lists.
- LameS[ν,j,z,0]=Sin[j(
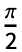 -z)].
-z)]. - LameS[ν,j,z,m] is proportional to HeunG[a,q,α,β,γ,δ,ξ], where
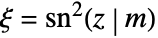 , if the parameters of HeunG are specialized as follows:
, if the parameters of HeunG are specialized as follows: 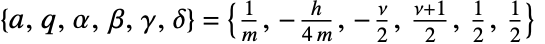 .
.
Examples
open allclose allBasic Examples (3)
Scope (27)
Numerical Evaluation (5)
Specific Values (3)
Visualization (6)
Plot the first three even LameS functions:
Plot the first three odd LameS functions:
Plot the absolute value of the LameS function for complex parameters:
Plot LameS as a function of its first parameter ![]() :
:
Plot LameS as a function of ![]() and elliptic parameter
and elliptic parameter ![]() :
:
Plot the family of LameS functions for different values of the elliptic parameter ![]() :
:
Function Properties (2)
Differentiation (3)
The ![]() -derivative of LameS is LameSPrime:
-derivative of LameS is LameSPrime:
Higher derivatives of LameS are calculated using LameSPrime:
Derivatives of LameS for specific cases of parameters:
Integration (3)
Series Expansions (3)
Function Representations (2)
Applications (1)
LameS solves the Lamé differential equation when h=LameEigenvalueB[ν,j,m]:
Properties & Relations (2)
LameS is an even function when ![]() is a positive odd integer:
is a positive odd integer:
LameS is an odd function when ![]() is a positive even integer:
is a positive even integer:
Use FunctionExpand to expand LameS for integer values of ![]() and
and ![]() :
:
Text
Wolfram Research (2020), LameS, Wolfram Language function, https://reference.wolfram.com/language/ref/LameS.html.
CMS
Wolfram Language. 2020. "LameS." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LameS.html.
APA
Wolfram Language. (2020). LameS. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LameS.html