LandauDistribution
LandauDistribution[μ,σ]
表示定位参数为 μ 和尺度参数为 σ 的 Landau 分布.
表示位置参数为0 、尺度参数为1的朗道分布.
更多信息
- 在 Landau 分布中,
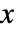 的概率密度与
的概率密度与 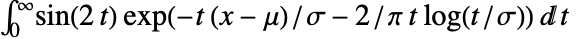 成正比.
成正比. - LandauDistribution 允许 μ 为任意实数,σ 为任意正实数.
- LandauDistribution 可与函数 Mean、CDF 和 RandomVariate 一起使用.
背景
- LandauDistribution[μ,σ] 表示一个定义于并支持在实数集
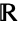 上、由实数 μ(称作“位置参数”)和实数 σ (称作“尺度参数”)参数化的统计分布. 总的来说,尽管总体形状(高度、延伸和
上、由实数 μ(称作“位置参数”)和实数 σ (称作“尺度参数”)参数化的统计分布. 总的来说,尽管总体形状(高度、延伸和  轴附近的集中)是由 μ 和 σ 的值决定的,一个 Landau 分布的概率密度函数(PDF)是单峰的,也就是说只有一个“峰值”(比如全局的最大值). 另外,对于较大的
轴附近的集中)是由 μ 和 σ 的值决定的,一个 Landau 分布的概率密度函数(PDF)是单峰的,也就是说只有一个“峰值”(比如全局的最大值). 另外,对于较大的 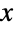 值 PDF 呈代数而非指数降低,就此意义而言 PDF 的尾部是“胖的”.(这种行为在可以再在较大
值 PDF 呈代数而非指数降低,就此意义而言 PDF 的尾部是“胖的”.(这种行为在可以再在较大 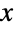 的 PDF 的重对数坐标图(LogLogPlot)的“本地线性行为”中观察到.)零自变量形式 LandauDistribution[] (等价于 LandauDistribution[0,1])有时也被称作标准 Landau 分布.
的 PDF 的重对数坐标图(LogLogPlot)的“本地线性行为”中观察到.)零自变量形式 LandauDistribution[] (等价于 LandauDistribution[0,1])有时也被称作标准 Landau 分布. - Landau 分布是由苏联物理学家在1944年的论文中作为适用于描述“快速”粒子(即所含能量足够使离子化理论可以应用)贯穿一层固定态物质(较小)厚度时的能量流失过程的广义分布发表的. 同样,Landau 分布可以对物理和化学的子领域中的很多现象建模.
- RandomVariate 可用于从一个 Landau 分布中给出一个或多个机器精度或任意精度(后者通过 WorkingPrecision 选项)伪随机变量. Distributed[x,LandauDistribution[μ,σ]],更简洁地写作 xLandauDistribution[μ,σ],可用于声明一个随机变量 x 的分布是依据 Landau 分布的. 这样的声明可用于如 Probability、 NProbability、 Expectation 和 NExpectation 等函数.
- Landau 分布的概率密度和累计分布函数可以通过 PDF[LandauDistribution[μ,σ],x] 和 CDF[LandauDistribution[μ,σ],x] 给出. 均值、中位数、方差、原始矩和中心矩分别可以通过 Mean、 Median、 Variance、 Moment 和 CentralMoment 计算出,但是由于其较长的尾部, LandauDistribution 的
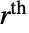 原始矩和中心矩(包括均值和方差)对于
原始矩和中心矩(包括均值和方差)对于 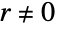 都是 Indeterminate.
都是 Indeterminate. - DistributionFitTest 可用于测试给定数据集是否符合 Landau 分布, EstimatedDistribution 可用于从给定数据中估计 Landau 参数分布,而 FindDistributionParameters 可用于拟合数据至一个 Landau 分布. ProbabilityPlot 可用于生成给定数据的 CDF 对符号 Landau 分布的 CDF 的图像,而 QuantilePlot 可用于生成给定数据的分位数对符号 Landau 分布的分位数的图像.
- TransformedDistribution 可用于表示一个变形 Landau 分布,CensoredDistribution 可用于表示在上限和下限之间的删节值的分布,TruncatedDistribution 可用于表示上限和下限之间的截尾值的分布. CopulaDistribution 可用于构建包含 Landau 分布的更高维度的分布,而 ProductDistribution 可用于计算涉及 Landau 分布的有独立组分分布的联合分布.
- LandauDistribution 与很多其他分布紧密相关. 例如, LandauDistribution 是1类 StableDistribution 的特殊情况,就此意义而言 LandauDistribution[μ,σ] 的 PDF 与 StableDistribution[1,1,1,μ,σ] 的 PDF 完全相同. 因此,LandauDistribution 也在数量上与一些分布相关,这样的分布包括 CauchyDistribution、 LevyDistribution 和 NormalDistribution.
范例
打开所有单元关闭所有单元范围 (4)
应用 (2)
假设带电粒子冲撞一个非常单薄的目标. 则 LandauDistribution 可用来描述能量损失谱. 定义 Landau 函数![]() :
:
属性和关系 (4)
Wolfram Research (2010),LandauDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LandauDistribution.html (更新于 2016 年).
文本
Wolfram Research (2010),LandauDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/LandauDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2010. "LandauDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/LandauDistribution.html.
APA
Wolfram 语言. (2010). LandauDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LandauDistribution.html 年