LessEqual

x<=y または x≤y

x が y より小さいか等しいと判断されると，Trueを返す．

x1≤x2≤x3

が広義の単調増加列である場合にTrueを返す．

詳細

  • LessEqualは，弱不等式あるいは非厳密な不等式としても知られている．
  • x≤y は，x <= y または x \[LessEqual]y と入力できる．
  • LessEqualは，引数が実数のときに，TrueまたはFalseを返す．
  • LessEqualは，引数が数ではない場合，簡約化を行う．
  • 厳密な数に対して，LessEqualは数値的順序付けを行うため内部で数値近似を行う．このため，大域変数$MaxExtraPrecisionの設定に影響を受ける．
  • StandardFormにおいて，LessEqualは≤の形で表示される．
  • x </ y または x \[LessSlantEqual] y という形式で入力された x≤y は，x≤y の代りとして入力の際に使用することができる．

例題

すべて開くすべて閉じる

例  (2)

数を比べる：

不等式を表す：

スコープ  (9)

数値不等式  (7)

不等式は実数についてのみ定義される：

有理数を比べる：

最高で二進数の最後の8桁しか違わない近似数は等しいとみなされる：

厳密数の式と近似数を比較する：

2つの厳密な数式を比較する．数値テストはこの不等式の証明には十分かもしれない：

この不等式の証明には記号的なメソッドが必要である：

LessEqualが使う記号・数値メソッドはこの不等式の証明には不十分である：

RootReduceを使って代数的数の符号を判断する：

LessEqualが使う数値メソッドはこの不等式が成り立たないことを証明するのに十分な精度ではない：

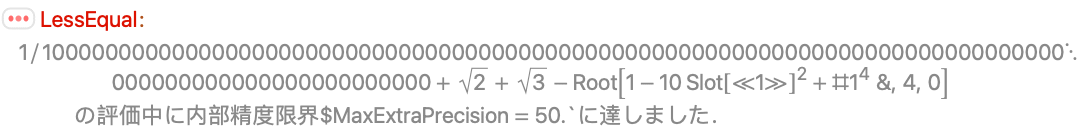
RootReduce は厳密なメソッドを使って不等式が成り立たないことを証明する：

$MaxExtraPrecisionの値を大きくすると不等式が成り立たないことを証明できるかもしれない：

記号不等式  (2)

x が実数ではないかもしれないので，記号不等式は未評価で残される：

Refineを使って x が実数だと仮定し，この不等式を再評価する：

記号不等式：

Reduceを使って解集合の明示的な記述を求める：

FindInstanceを使って解の例を求める：

Minimizeを使って不等式で定義された範囲で最適化する：

Refineを使って不等式で定義された仮定の下で簡約する：

特性と関係  (12)

2引数のLessEqualの否定はGreaterである：

3引数のLessEqualの否定は自動的には簡約されない：

LogicalExpandを使って2引数のGreaterについてこれを表現する：

これは3引数のGreaterとは等価ではない：

LessEqualが数式間の不等式を判断できないとき，不等式は未評価で返される：

FullSimplifyは厳密な記号変換を使って不等式を証明する：

NonPositive[x]はと等価である：

Reduceを使って不等式を解く：

FindInstanceを使って解の例を求める：

RegionPlotとRegionPlot3Dを使って不等式の解集合を可視化する：

不等式による仮定：

MinimizeとMaximizeを使って不等式によって制約された最適化問題を解く：

NMinimizeとNMaximizeを使って制約条件付きの最適化問題を数値的に解く：

不等式の解集合上で関数を積分(Integrate)する：

Median，Quantile，Quartilesを 番目の最大数に使う：

考えられる問題  (3)

機械精度の近似数の不等式は微妙なこともある：

結果は余分な桁に基づいている：

任意精度の近似数にはこの問題はない：

自動精度追跡機能のお陰で，LessEqualは最初の10桁だけを見ればよいと知っている：

この場合，機械数間の不等式は予期した結果を返す：

この場合の余分桁はLessEqualに無視される：

Wolfram Research (1988), LessEqual, Wolfram言語関数， https://reference.wolfram.com/language/ref/LessEqual.html （1996年に更新）.

テキスト

Wolfram Research (1988), LessEqual, Wolfram言語関数， https://reference.wolfram.com/language/ref/LessEqual.html （1996年に更新）.

CMS

Wolfram Language. 1988. "LessEqual." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/LessEqual.html.

APA

Wolfram Language. (1988). LessEqual. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LessEqual.html

BibTeX

@misc{reference.wolfram_2024_lessequal, author="Wolfram Research", title="{LessEqual}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/LessEqual.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_lessequal, organization={Wolfram Research}, title={LessEqual}, year={1996}, url={https://reference.wolfram.com/language/ref/LessEqual.html}, note=[Accessed: 22-November-2024 ]}