LessEqual

x<=y 或 x≤y

如果判断 x 小于或等于 y，产生 True.

x1≤x2≤x3

如果 形成一个非递减序列，产生 True.

更多信息

范例

打开所有单元关闭所有单元

基本范例  (2)

数字比较：

表示一个不等式：

范围  (9)

数值不等式  (7)

仅对实数定义不等式：

有理数比较：

仅在至多最后 8 个二进制数位不相同的近似数被认为是相等的：

比较明确的数值表达式和一个近似数：

比较两个明确的数值表达式；一个数值测试足以证明不等性：

对这个不等式的反证需要符号方法：

用 LessEqual 的符号方法和数值方法不足以反证这个不等式：

用 RootReduce 确定代数数的符号：

LessEqual 使用的数值方法没有提供足够的精度来证明这个不等式：

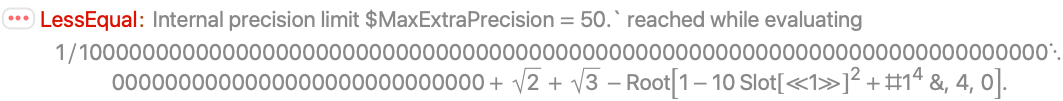
RootReduce 用明确的方法证明不等式：

增加 $MaxExtraPrecision 也可以证明这个不等式：

符号不等式  (2)

若 x 不是一个实数，符号不等式保持不计算的形式：

假定 x 是一个实数，用 Refine 重新计算不等式：

一个符号不等式：

用 Reduce 求解集的一个明确描述：

用 FindInstance 求一个实例：

在不等式定义的区域上，用 Minimize 优化：

在不等式定义的假设条件下，用 Refine 化简：

属性和关系  (12)

二元参数 LessEqual 的否定形式是 Greater：

三元参数 LessEqual 的否定形式不能自动化简：

通过 LogicalExpand 用二元参数 Greater 来表示它：

这不等于三元参数 Greater：

当 LessEqual 不能确定数值表达式之间的不等性时，将返回原式：

FullSimplify 用精确的符号转换来证明这个不等式：

NonPositive[x] 等价于 ：

用 Reduce 求解不等式：

用 FindInstance 求一个实例：

用 RegionPlot 和 RegionPlot3D 可视化显示不等式的解集：

不等式假设：

用 Minimize 和 Maximize 来求解不等式约束条件下的优化问题：

用 NMinimize 和 NMaximize 数值求解约束条件下的优化问题：

在不等式解集上的对函数进行 Integrate 操作：

将 Median，Quantile 和 Quartiles 用于 个最大数：

可能存在的问题  (3)

机器精度数之间的不等性可以很精确：

严格的不等式是基于额外的数字：

任意精度的近似数没有这个问题：

由于自动精度跟踪，LessEqual 明确前 10 个数位：

在这个例子中，机器数之间的不等式给出预期结果：

在这个例子中额外的数字被 LessEqual 忽略：

Wolfram Research (1988)，LessEqual，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LessEqual.html （更新于 1996 年）.

文本

Wolfram Research (1988)，LessEqual，Wolfram 语言函数，https://reference.wolfram.com/language/ref/LessEqual.html （更新于 1996 年）.

CMS

Wolfram 语言. 1988. "LessEqual." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 1996. https://reference.wolfram.com/language/ref/LessEqual.html.

APA

Wolfram 语言. (1988). LessEqual. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/LessEqual.html 年

BibTeX

@misc{reference.wolfram_2024_lessequal, author="Wolfram Research", title="{LessEqual}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/LessEqual.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_lessequal, organization={Wolfram Research}, title={LessEqual}, year={1996}, url={https://reference.wolfram.com/language/ref/LessEqual.html}, note=[Accessed: 22-November-2024 ]}