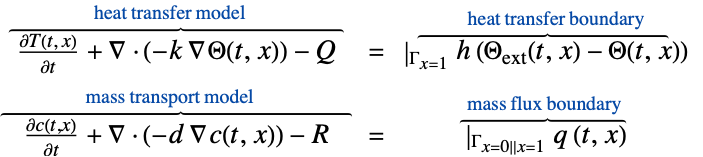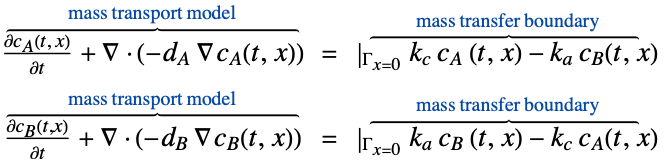MassTransportPDEComponent[vars,pars]
変数 vars,パラメータ pars の物質移動PDE項を与える.




MassTransportPDEComponent
MassTransportPDEComponent[vars,pars]
変数 vars,パラメータ pars の物質移動PDE項を与える.
詳細





- MassTransportPDEComponentは,偏微分方程式の一部として使われる微分演算子の和を返す.
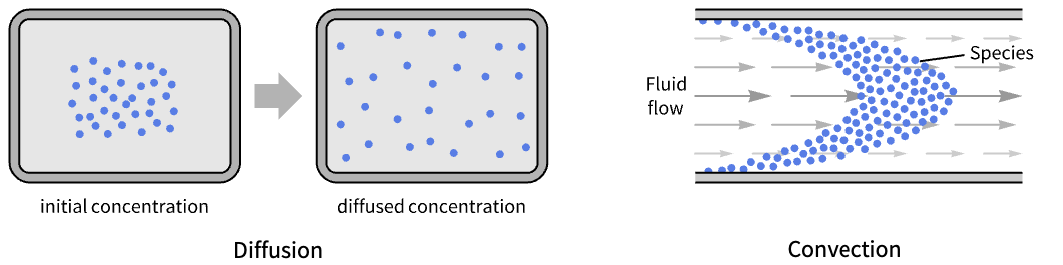
- MassTransportPDEComponentは,物理系における混合物,溶液,固体等の希釈された物質種の,対流や拡散等のメカニズムによる生成や伝播をモデル化する.
- MassTransportPDEComponentモデルは,希釈種の濃度が溶媒の濃度よりも少なくとも1桁小さい場合には適用可能である.
- MassTransportPDEComponentは,物質の移動現象を,従属変数
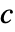 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/", , {"m", ^, 3}}, moles per meter cubed, {{(, "Moles", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/MassTransportPDEComponent.ja/4.png) ]),独立変数
]),独立変数 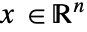 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/MassTransportPDEComponent.ja/6.png) ]),時間変数
]),時間変数 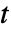 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/MassTransportPDEComponent.ja/8.png) ])でモデル化する.
])でモデル化する. - 定常変数 vars は vars={c[x1,…,xn],{x1,…,xn}}である.
- 時間依存変数 vars は vars={c[t,x1,…,xn],t,{x1,…,xn}}である.
- MassTransportPDEComponentは,圧縮性流れで使う保存型のモデルと非圧縮性流れて使う非保存型のモデルの両方を提供する.
- 非保存型時間依存物質移動PDE MassTransportPDEComponentは,質量拡散率
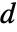 ,物質対流速度ベクトル
,物質対流速度ベクトル 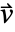 ,質量反応率
,質量反応率 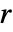 ,物質源項
,物質源項 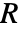 の対流拡散モデルに基づいている.
の対流拡散モデルに基づいている. - 保存型時間依存物質移動モデルMassTransportPDEComponentは,以下で与えられる保存型の対流拡散項に基づいている.
- 非保存型の定常物質移動PDE項は以下で与えられる.
- 非保存型モデルの陰的なデフォルトの境界条件はMassOutflowValueである.
- 保存型の定常物質移動PDE項は以下で与えられる.
- 保存型モデルのための陰的なデフォルトの境界条件はMassImpermeableBoundaryValueである.
- 非保存型と保存型のモデルの差は,対流速度
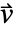 の扱いにある.
の扱いにある. - 非保存型モデルがデフォルトモデルである.対流速度
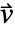 の発散が非零のときには保存型モデルを使うべきである.
の発散が非零のときには保存型モデルを使うべきである. - 物質移動PDE項の単位は[
![TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , {"m", ^, 3}, , "s", , ")"}, moles per meter cubed second, {{(, "Moles", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , {"m", ^, 3}, , "s", , ")"}, moles per meter cubed second, {{(, "Moles", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF]](Files/MassTransportPDEComponent.ja/19.png) ]である.
]である. - 以下のモデルパラメータ pars を与えることができる.
-
パラメータ デフォルト シンボル "MassConvectionVelocity" 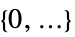
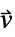 ,流速(単位:[
,流速(単位:[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/MassTransportPDEComponent.ja/22.png) ])
])"DiffusionCoefficient" IdentityMatrix 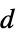 ,質量拡散率(単位:[
,質量拡散率(単位:[![TemplateBox[{InterpretationBox[, 1], {{"m", ^, 2}, , "/", , "s"}, meters squared per second, {{(, {"Meters", ^, 2}, )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {{"m", ^, 2}, , "/", , "s"}, meters squared per second, {{(, {"Meters", ^, 2}, )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/MassTransportPDEComponent.ja/24.png) ])
])"MassReactionRate" 0 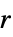 ,質量反応率(単位:[1/
,質量反応率(単位:[1/![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/MassTransportPDEComponent.ja/26.png) ])
])"MassSource" 0 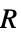 ,物質源(単位:[
,物質源(単位:[![TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , {"m", ^, 3}, , "s", , ")"}, moles per meter cubed second, {{(, "Moles", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF]] TemplateBox[{InterpretationBox[, 1], {"mol", , "/(", , {"m", ^, 3}, , "s", , ")"}, moles per meter cubed second, {{(, "Moles", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF]]](Files/MassTransportPDEComponent.ja/28.png) )
)"ModelForm" "NonConservative" 
"RegionSymmetry" None 
- パラメータはどれも任意の
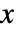 ,
,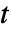 ,
,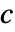 あるいはその他の従属変数に依存するかもしれない.
あるいはその他の従属変数に依存するかもしれない. - 独立変数の個数
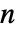 は
は 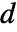 の次元と
の次元と 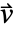 の長さを決定する.
の長さを決定する. - 物質対流速度は,流体が物質を輸送する速度
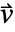 を指定する.
を指定する. - 質量反応項
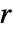 は質量の質量化学反応をモデル化する.
は質量の質量化学反応をモデル化する. - 物質源
 は系から生成された(正)または吸収された(負)物質をモデル化する.
は系から生成された(正)または吸収された(負)物質をモデル化する. - パラメータ"ModelForm"の可能な選択肢は"Conservative"と"NonConservative"である.
- パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある.
- "Axisymmetric"領域対称性は,以下のように角度変数を削除することで円柱座標が縮小された切取り円柱座標系を表す.
-
次元 縮小 非保存型方程式 1D 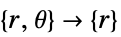
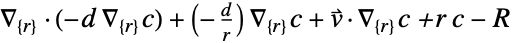
2D 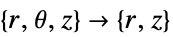
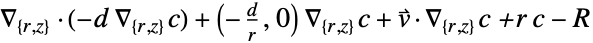
-
次元 縮小 保存型方程式 1D 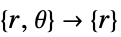
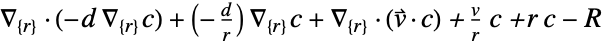
2D 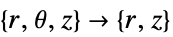

- パラメータの入力指定は対応する演算子形のそれと全く同じである.
- 対応する演算子項と同じ入力指定で連立方程が生成できる.
- パラメータが指定されていない場合のデフォルトの質量物質移動PDEは以下の通りである.
- MassTransportPDEComponentが…,keypi…,pivi,…として連想 pars で指定されるパラメータ
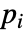 に依存するなら,パラメータ
に依存するなら,パラメータ 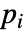 は
は 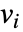 で置換される.
で置換される.
例題
すべて開く すべて閉じる例 (3)
スコープ (23)
基本的な用法 (9)
1D (1)
2D (2)
3D (1)
材料領域 (1)
時間依存 (1)
非線形時間依存 (1)
結合時間依存 (2)
1Dの非保存型結合双対化学種場を,境界の左の部分を通る対応する質量流束でモデル化する:
種 ![]() と
と ![]() それぞれについて時間依存物質移動モデル変数 vars を設定する:
それぞれについて時間依存物質移動モデル変数 vars を設定する:
種 ![]() と
と ![]() それぞれについて物質移動モデルパラメータ質量拡散率
それぞれについて物質移動モデルパラメータ質量拡散率 ![]() と
と ![]() を指定する:
を指定する:
最初の50秒間の左端の質量流束 ![]() (
(![]() が4
が4 ![]() ,
,![]() が8
が8 ![]() )で境界条件を設定する:
)で境界条件を設定する:
1D結合化学種場を,左境界を通る対流速度と質量流速でモデル化する:
種 ![]() と
と ![]() それぞれについて時間依存物質移動モデル変数 vars を設定する:
それぞれについて時間依存物質移動モデル変数 vars を設定する:
種 ![]() と
と ![]() それぞれについて物質移動モデルパラメータ質量拡散率
それぞれについて物質移動モデルパラメータ質量拡散率 ![]() と
と ![]() を指定する:
を指定する:
アプリケーション (7)
単一の方程式 (4)
以下の物質移動モデルは超遠心分離下でのディスクセクタセルの溶質の沈降と拡散を表している.この現象を説明する支配方程式はLamm方程式と呼ばれるが,これは1D軸対称保存型物質移動方程式でモデル化できる:
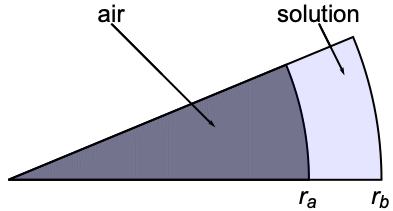
![]() が遠心分離過程で形成される空気溶液メニスカスの半径方向の位置,
が遠心分離過程で形成される空気溶液メニスカスの半径方向の位置,![]() がセルの底の半径位置を表す線形領域
がセルの底の半径位置を表す線形領域![]() を設定する:
を設定する:
モデルのパラメータ種拡散係数 ![]()
![]() と流体の流速
と流体の流速 ![]() を指定する.ここで,
を指定する.ここで,![]() は沈降係数(
は沈降係数(![]() ),
),![]() は角速度(
は角速度(![]() )である:
)である:
流束は領域の両境界で0なので,使用される境界条件は ![]() で適用されるMassImpermeableBoundaryValueである.この特定の境界は保存型モデルの陰的デフォルト境界条件である.
で適用されるMassImpermeableBoundaryValueである.この特定の境界は保存型モデルの陰的デフォルト境界条件である.
汚染物質の物質移動を等方性均質媒体内の2Dの矩形領域でモデル化する.最初は,関心領域全体で汚染物質濃度は0である.左境界の中央では0.2 ![]() の帯状に3000
の帯状に3000 ![]() の濃度が維持される.一方,上下の境界には
の濃度が維持される.一方,上下の境界には![]() の汚染物質の流出が適用される.0.833
の汚染物質の流出が適用される.0.833 ![]() の拡散係数が一様に分布するが,水平速度と垂直速度のどちらも空間に依存する:
の拡散係数が一様に分布するが,水平速度と垂直速度のどちらも空間に依存する:
フォッカー・プランク(Fokker–Planck)方程式を設定する:
モデルパラメータ種拡散率 ![]() ,対流速度項,パラメータを指定する:
,対流速度項,パラメータを指定する:
この場合,フォッカー・プランク方程式を解くためには一次メッシュで十分である.より高次のメッシュを使うとメモリ消費量が大きくなる.解いている間,NDSolveは偏微分方程式の対流が支配的な性質について警告する:
スモルコフスキー(Smoluchowski)の拡散方程式はフォッカー・プランク方程式の特殊ケースである.どちらの方程式も保存型の物質移動方程式でモデル化できる:
F(x)=-∇xU(x)で F(x)と関連した線形ポテンシャル U(x)に依存するモデルパラメータ種拡散率 ![]() と移動期間を指定する:
と移動期間を指定する:
特性と関係 (1)
考えられる問題 (2)
陰的デフォルト境界条件はモデルの形式によって変化する.保存型のモデルについては,陰的ノイマン(Neumann)0の境界条件は不透過境界条件を指定することと同じである.非保存型のモデルについては,陰的ノイマン0の境界条件は流出境界条件を指定することと同じである.
等速場については,保存型と非保存型の両方のモデルが同じ結果を返す.保存型と非保存型の場の比較は以下のモデルに基づいて行われる:
保存型モデルについてのデフォルトの境界条件は不透過境界なので,非保存型モデルに不透過境界条件が加えられる:
解の差のスケールは予想されるもので,演算子が計算される方法の数値誤差に由来する.
離散化された領域が与えられ,メッシュが大きい対流拡散比の品質基準を満たさない場合は,メッセージが生成される.次のように表される高い対流速度と拡散率の比で,1D非保存型化学種場をモデル化する:
テクニカルノート
-
▪
- 物質輸送
関連するガイド
テキスト
Wolfram Research (2020), MassTransportPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/MassTransportPDEComponent.html (2021年に更新).
CMS
Wolfram Language. 2020. "MassTransportPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/MassTransportPDEComponent.html.
APA
Wolfram Language. (2020). MassTransportPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MassTransportPDEComponent.html
BibTeX
@misc{reference.wolfram_2025_masstransportpdecomponent, author="Wolfram Research", title="{MassTransportPDEComponent}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/MassTransportPDEComponent.html}", note=[Accessed: 01-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_masstransportpdecomponent, organization={Wolfram Research}, title={MassTransportPDEComponent}, year={2021}, url={https://reference.wolfram.com/language/ref/MassTransportPDEComponent.html}, note=[Accessed: 01-March-2026]}