WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

MatrixTDistribution

MatrixTDistribution[Σ_row,Σ_col,ν]

行の共分散行列 Σ_row，列の共分散行列 Σ_col，自由度母数 ν のゼロ平均行列分布を表す．

MatrixTDistribution[μ,Σ_row,Σ_col,ν]

平均行列が μ の行列分布を表す．

詳細

行列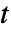分布における次元が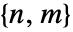である行列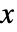の確率密度は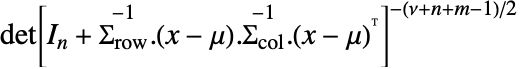に比例する．ただし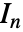，は長さ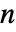の恒等行列である．
MatrixTDistribution[Σ_row,Σ_col,ν]はMatrixNormalDistribution[Σ,Σ_col]の分布である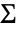．はInverseWishartMatrixDistribution[ν+n-1,Σ_row]からサンプルされている．
MatrixTDistribution[μ,c Σ_row,c^-1 Σ_col,ν]は，任意の正の実数定数cについては，MatrixTDistribution[μ,Σ_row,Σ_col,ν]と同じ分布を持つ．
共分散行列 Σ_rowおよび Σ_colは，次元がそれぞれ{n,n}および{m,m}の実数値の任意の正定値対称行列である．自由度母数 ν は任意の正の数でよく，平均行列 μ は次元が{n,m}の実数の任意の行列でよい．
MatrixTDistributionは，MatrixPropertyDistribution，EstimatedDistribution，RandomVariate等の関数とともに使うことができる．

例題

すべて開くすべて閉じる

例 (2)

行列分布からサンプルする：

平均と分散：

スコープ (6)

単一の擬似ランダム行列を生成する：

平均が非零である単一の擬似ランダム行列を生成する：

擬似ランダム行列の集合を生成する：

拡張精度でサンプルする：

分布母数推定：

サンプルデータから分布母数を推定する：

両分布のLogLikelihoodを比較する：

歪度と尖度：

確率密度関数：

対角行列の確率密度関数をプロットする：

特性と関係 (4)

行列 t 分布は正の乗数に対して定義される：

尺度行列の行と列が正の定数で乗除された同等の分布：

ランダムな点における分布の確率密度関数を計算する：

MatrixTDistribution[Σ_row,Σ_col,ν]はMatrixNormalDistribution[Σ,Σ_col]の母数混合分布である．ただし，はInverseWishartMatrixDistribution[ν+n-1,Σ_row]に従う：

MatrixNormalDistributionとInverseWishartMatrixDistributionの母数混合分布に従うサンプルを作る：

サンプルデータをMatrixTDistributionにフィットする：

適切なMatrixTDistributionに対する対数尤度比統計を計算する：

対数尤度比は，母数が自由度の数に等しいChiSquareDistributionに従う：

尤度比検定の値を計算する：

行列分布からサンプルされた行列については，式は長さがの次元にマッチする任意の非零のベクトルおよびについてスチューデント分布に従う：

MatrixPropertyDistributionを使って式の値をサンプルする：

期待される分布との一致をチェックする：

行列分布からサンプルされた行列については，は長さがの列数にマッチする任意の非零のベクトルについて多変量分布に従う：

MatrixPropertyDistributionを使っての値をサンプルする：

期待される分布との適合度を確かめる：

考えられる問題 (1)

行列分布は正の乗数に対して定義される．推定母数はもとになる分布を指定する母数に近くはないかもしれない：

行列分布からのサンプル：

分布を推定する：

推定された尺度母数をもとになっている分布のそれと比較する：

尺度行列のクロネッカー(Kronecker)積は互いに近い：

分布のLogLikelihoodは推定が適切であることを示している：

トップへ