Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

MatrixTDistribution

MatrixTDistribution[Σ_row,Σ_col,ν]

表示零均值矩阵分布，其中行协方差矩阵为 Σ_row，列协方差矩阵为 Σ_col，自由度参数为 ν.

MatrixTDistribution[μ,Σ_row,Σ_col,ν]

表示均值矩阵为 μ 的矩阵分布.

更多信息

在矩阵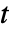分布中，维度为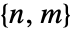的矩阵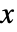的概率密度与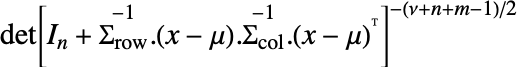成正比，其中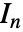是一个长度为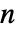的单位矩阵.
MatrixTDistribution[Σ_row,Σ_col,ν] 是 MatrixNormalDistribution[Σ,Σ_col] 的分布，其中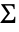是取自 InverseWishartMatrixDistribution[ν+n-1,Σ_row] 的样本.
对于任意正的实常数 c，MatrixTDistribution[μ,c Σ_row,c^-1 Σ_col,ν] 与 MatrixTDistribution[μ,Σ_row,Σ_col,ν] 分布相同.
协方差矩阵 Σ_row 和 Σ_col 是维度分别为 {n,n} 和 {m,m} 的任意实数对称正定矩阵. 自由度参数 ν 可以是任意正实数，均值矩阵 μ 可以是维度为 {n,m} 的任意实数矩阵.
MatrixTDistribution 可与如 MatrixPropertyDistribution、EstimatedDistribution 和 RandomVariate 这样的函数一起使用.

范例

打开所有单元关闭所有单元

基本范例 (2)

从矩阵分布取样：

均值和方差：

范围 (6)

生成单个伪随机矩阵：

生成均值非零的单个伪随机矩阵：

生成一组伪随机矩阵：

提高精度：

分布参数估计：

根据抽样数据估计分布参数：

比较两个分布的 LogLikelihood：

偏度和峰度：

概率密度函数：

绘制对角矩阵的 PDF：

属性和关系 (4)

用正的倍增常数定义矩阵 t 分布：

将行和列尺度矩阵乘以和除以一个正的常数所得的等价分布：

计算分布的 PDF 在一个随机点的值：

MatrixTDistribution[Σ_row,Σ_col,ν] 是 MatrixNormalDistribution[Σ,Σ_col] 的参数混合分布，其中服从 InverseWishartMatrixDistribution[ν+n-1,Σ_row]:

产生一个服从 MatrixNormalDistribution 和 InverseWishartMatrixDistribution 的参数混合分布的样本：

把样本数据拟合到 MatrixTDistribution：

计算与相应的 MatrixTDistribution 相比所得的对数似然比统计量：

对数似然比服从 ChiSquareDistribution，其中的参数等于自由度的数量：

计算对数似然比检验的 -值：

服从矩阵分布的样本矩阵，表达式服从学生分布，其中非零向量和的长度均与的大小匹配：

使用 MatrixPropertyDistribution 对表达式的值取样：

检查与期望分布的一致性：

对于服从矩阵分布的样本矩阵，服从多元分布，其中非零向量的长度与的列数匹配：

使用 MatrixPropertyDistribution 对表达式的值取样：

验证与期望分布的拟合优度：

可能存在的问题 (1)

可用倍增尺度常数定义矩阵分布. 估计参数可能与指定基本分布的参数不太一样：

从矩阵分布中抽样：

估计分布：

比较估计的尺度参数与基本分布的尺度参数:

尺度矩阵的克罗内克积较为接近:

分布的 LogLikelihood 表明这是一个成功的估计：

顶部