Modulus

Modulusn

代数関数等のオプションとして使われ，整数を n を法として取り扱うように指定する．

詳細

  • Modulusは，Inverse，LinearSolve，Det等の線形代数関数と，Solve，Reduce，Factor，PolynomialGCD，PolynomialLCMにおけるオプションとして使われる．
  • 算術的な計算は，通常，整数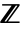の全環上で行われる．オプションModulusを設定することで，この計算が有限な環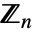上で行われることを指定する．
  • Modulus->0の設定は，整数の全環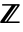を指定する．
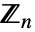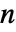  • 関数によっては，Modulusが素であることや素のベキであることが要求される．は， が素数である場合に有限体となる．
  • Modulusの方程式は，Eliminateおよび関連関数によって与えられる．

例題

すべて開くすべて閉じる

例  (1)

方程式を解く：

多項式を因数分解する：

逆関数を計算する：

スコープ  (6)

2を法とした整数上でPolynomialGCDを計算する：

3を法とした整数上で多項式を因数分解(Factor)する：

5を法とした整数上でGroebnerBasisを求める：

7を法とした整数上で方程式を簡約(Reduce)する：

8を法とした行列の行列式を計算する：

方程式系が解を持つ法を求める：

特性と関係  (2)

多項式を有限体上で因数分解(Factor)する：

有理数の有限拡大(Extension)上で多項式を因数分解(Factor)する：

Wolfram Research (1988), Modulus, Wolfram言語関数， https://reference.wolfram.com/language/ref/Modulus.html.

テキスト

Wolfram Research (1988), Modulus, Wolfram言語関数， https://reference.wolfram.com/language/ref/Modulus.html.

CMS

Wolfram Language. 1988. "Modulus." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Modulus.html.

APA

Wolfram Language. (1988). Modulus. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Modulus.html

BibTeX

@misc{reference.wolfram_2024_modulus, author="Wolfram Research", title="{Modulus}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Modulus.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_modulus, organization={Wolfram Research}, title={Modulus}, year={1988}, url={https://reference.wolfram.com/language/ref/Modulus.html}, note=[Accessed: 22-November-2024 ]}