NegativelyOrientedPoints
NegativelyOrientedPoints[{p1,p2,p3,…,pn}]
点の列 p1,p2,p3,…,pnが負の向きかどうかを調べる.
詳細

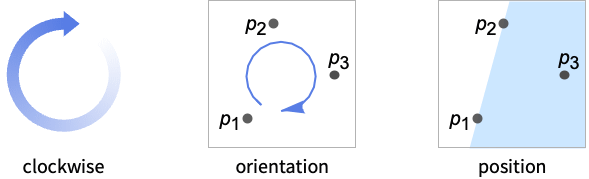
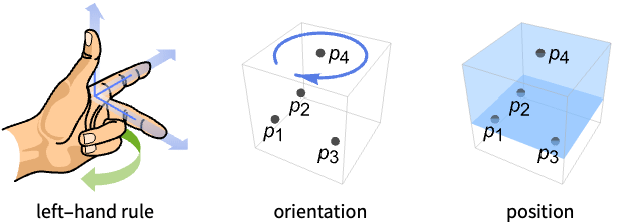
- NegativelyOrientedPointsは,2Dでは時計回り方向,3Dでは左手の法則としても知られている.
- 回転運動の点集合に関する方向を決定するためによく使われる.
- NegativelyOrientedPoints[{p1,p2,p3}]は,二次元では,点 p3が p1と p2を通る線で有界で{1,0}方向に伸びている半平面にある場合はTrueを与える.
- 行列{p2-p1, p3-p1}の行列式は,負の向きにある p1,p2,p3について負である.
- NegativelyOrientedPoints[{p1,p2,p3,p4}]は,三次元では,点 p4が p1を通る法線方向(p3-p1)(p2-p1)の平面で有界の半空間にある場合はTrueを与える.
- 負の向きの点 p1,p2,p3,p4について,p4-p1と(p3-p1)(p2-p1)のドット積は負である.
- d 次元における d+1個の点 p1,p2,…,pd+1は,行列{p2-p1,…,pd+1-p1}の行列式が負の場合は負の向きである.
例題
すべて開くすべて閉じるスコープ (3)
NegativelyOrientedPointsは二次元の点に使うことができる:
NegativelyOrientedPointsは数値座標に使うことができる:
座標の集合上のNegativelyOrientedPoints:
一般化と拡張 (1)
NegativelyOrientedPointsに仮定を加える:
アプリケーション (5)
幾何 (3)
2Dの直線上のNegativelyOrientedPoints:
NegativelyOrientedPointsの強靭さを示す:
特性と関係 (4)
NegativelyOrientedPointsは,共線の点に対してはFalseを返す:
NegativelyOrientedPointsは,正の向きに対してはFalseを返す:
RegionMemberを使って点が負の向きかどうかを調べる:
テキスト
Wolfram Research (2020), NegativelyOrientedPoints, Wolfram言語関数, https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html.
CMS
Wolfram Language. 2020. "NegativelyOrientedPoints." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html.
APA
Wolfram Language. (2020). NegativelyOrientedPoints. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NegativelyOrientedPoints.html