NeumannBoundaryUnitNormal
NeumannBoundaryUnitNormal[{x,y,…}]
represents an outward-pointing unit normal vector at the point ![]() on the boundary of a filled region.
on the boundary of a filled region.
Details


- NeumannBoundaryUnitNormal can be used to construct partial differential equation boundary conditions that depend on the unit normal vector
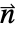 of the boundary.
of the boundary. - NeumannBoundaryUnitNormal can be used with NeumannValue, DirichletCondition and NIntegrate with the finite element method.
- NeumannBoundaryUnitNormal is used when non-normal flux values can be specified, like in AcousticRadiationValue or in ElectricCurrentDensityValue.
- NeumannBoundaryUnitNormal is generated by nonconservative boundary conditions for mass transport, like MassOutflowValue.
- For finite element approximations, the PDE is multiplied with a test function
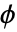 and integrated over
and integrated over 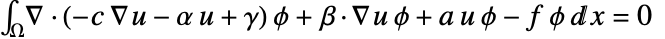 . Integration by parts gives
. Integration by parts gives 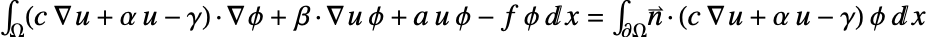 . The integrand
. The integrand 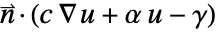 in the boundary integral is replaced with the NeumannValue
in the boundary integral is replaced with the NeumannValue 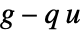 .
. - NeumannBoundaryUnitNormal can be used to model a boundary integration term of the form
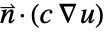 by specifying the NeumannValue as
by specifying the NeumannValue as 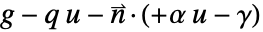 .
. - Conversely, when a PDE specifies a Neumann value as
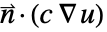 , NeumannBoundaryUnitNormal can be used to model a boundary integration term of the form
, NeumannBoundaryUnitNormal can be used to model a boundary integration term of the form 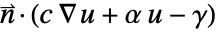 instead by specifying the NeumannValue as
instead by specifying the NeumannValue as 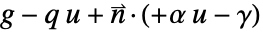 .
. - NeumannBoundaryUnitNormal will evaluate to a vector of length of the embedding dimension of the region
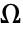 when the boundary condition is discretized.
when the boundary condition is discretized. - NeumannBoundaryUnitNormal can be used to derive the tangent line (2D) and tangent plane (3D).
- Components of the boundary unit normal
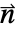 can be accessed with Indexed.
can be accessed with Indexed. - At internal boundaries of a region, the boundary unit normal is not uniquely defined.
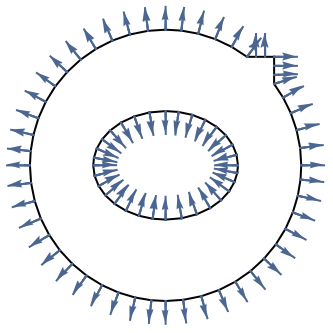
- The value of the boundary unit normal
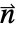 will be computed by solving
will be computed by solving 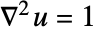 with a Dirichlet condition of
with a Dirichlet condition of 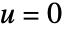 on all boundaries including internal boundaries over the entire region
on all boundaries including internal boundaries over the entire region 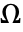 . The boundary unit normal is then the gradient of
. The boundary unit normal is then the gradient of 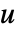 normalized with
normalized with 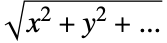 .
.
Examples
open allclose allBasic Examples (2)
Set up a symbolic electric current density boundary condition with a non-surface normal current density:
Specify a differential equation operator ![]() :
:
On the left, a NeumannValue is set up. The default Neumann boundary integrand for this equation is ![]() . To model a boundary integrand of the form
. To model a boundary integrand of the form ![]() , a NeumannValue
, a NeumannValue ![]() is set up:
is set up:
Scope (5)
For nonconservative mass transport, boundary conditions like MassImpermeableBoundaryValue can produce NeumannBoundaryUnitNormal. Set up an impermeable boundary condition for a nonconservative model:
NeumannBoundaryUnitNormal can be used in NIntegrate to compute the flux through a boundary. Solve a Poisson equation on a unit Disk:
Compute the total flux through the boundary of the region through the boundary region:
Compute the total flux through the boundary of a subregion:
Specify a time-dependent differential equation operator ![]() :
:
On the left, a NeumannValue is set up. The default Neumann boundary integrand for this equation is ![]() . To model a boundary integrand of the form
. To model a boundary integrand of the form ![]() , a NeumannValue
, a NeumannValue ![]() is set up:
is set up:
Use a Neumann 0 boundary condition and solve the equation again:
Inspect how the solutions start to differ over time:
Create a tangential for a NeumannValue:
Make use of an Indexed component, the ![]() component, of a NeumannBoundaryUnitNormal to compute a NeumannValue:
component, of a NeumannBoundaryUnitNormal to compute a NeumannValue:
Applications (1)
The AcousticRadiationValue makes use of a NeumannBoundaryUnitNormal to automatically compute the sound direction vector. Define model variables vars for a frequency domain acoustic pressure field with model parameters pars:
Set up the equation with a radiation boundary at the left end and an acoustic absorbing boundary at the right end:
Convert the solution to the time domain and visualize the solution in the frequency domain at various frequencies ![]() :
:
Properties & Relations (1)
The boundary unit normal is computed by solving a Poisson equation over the region and specifying 0 Dirichlet conditions. Compute a Poisson equation over a unit Disk:
Text
Wolfram Research (2025), NeumannBoundaryUnitNormal, Wolfram Language function, https://reference.wolfram.com/language/ref/NeumannBoundaryUnitNormal.html.
CMS
Wolfram Language. 2025. "NeumannBoundaryUnitNormal." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NeumannBoundaryUnitNormal.html.
APA
Wolfram Language. (2025). NeumannBoundaryUnitNormal. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NeumannBoundaryUnitNormal.html