NeumannBoundaryUnitNormal
NeumannBoundaryUnitNormal[{x,y,…}]
固体領域の境界上の点![]() における外向きの単位法線ベクトルを表す.
における外向きの単位法線ベクトルを表す.
詳細


- NeumannBoundaryUnitNormalを使って境界の単位法線ベクトル
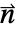 に依存する偏微分方程式境界条件が構築できる.
に依存する偏微分方程式境界条件が構築できる. - NeumannBoundaryUnitNormalは,有限要素法で,NeumannValue,DirichletCondition,NIntegrateと一緒に使うことができる.
- NeumannBoundaryUnitNormalは,AcousticRadiationValueやElectricCurrentDensityValueのように,非法線フラックス値が指定できる場合に使用される.
- NeumannBoundaryUnitNormalは,MassOutflowValueのような物質移動の非保存境界条件によって生成される.
- 偏微分方程式がテスト関数
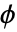 倍されて
倍されて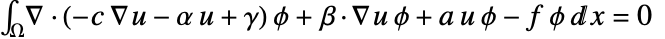 .上で積分される.部分積分は
.上で積分される.部分積分は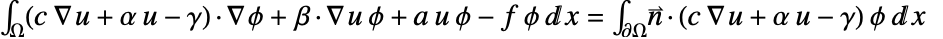 を与える.境界積分における被積分関数
を与える.境界積分における被積分関数 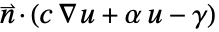 はNeumannValue
はNeumannValue 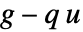 によって置換される.
によって置換される. - NeumannValueを
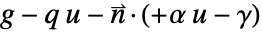 と指定することで,NeumannBoundaryUnitNormalを使って
と指定することで,NeumannBoundaryUnitNormalを使って 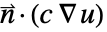 の形の境界積分項をモデル化することができる.
の形の境界積分項をモデル化することができる. - これとは逆に,PDEがノイマン(Neumann)値を
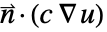 として指定する場合は,NeumannBoundaryUnitNormalを使用してNeumannValueを
として指定する場合は,NeumannBoundaryUnitNormalを使用してNeumannValueを 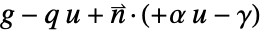 として指定することで
として指定することで 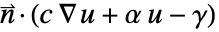 という形式の境界積分項がモデル化できる.
という形式の境界積分項がモデル化できる. - NeumannBoundaryUnitNormalは,境界条件が離散化されているときには,領域
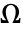 の埋込み次元の長さのベクトルとして評価される.
の埋込み次元の長さのベクトルとして評価される. - NeumannBoundaryUnitNormalを使って接線(2D)と接平面(3D)が導出できる.
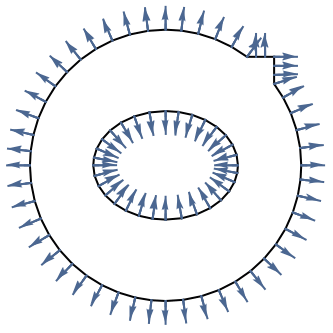
- 境界単位法線
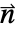 の成分にはIndexedでアクセスできる.
の成分にはIndexedでアクセスできる. - 領域の内部境界では,境界単位法線は一意的には定義されない.
- 境界単位法線
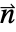 の値は,領域
の値は,領域 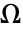 全体の内部境界を含むすべての境界上で
全体の内部境界を含むすべての境界上で 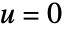 のディリクレ(Dirichlet)条件で
のディリクレ(Dirichlet)条件で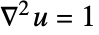 を解くことで計算される.したがって,境界単位法線は
を解くことで計算される.したがって,境界単位法線は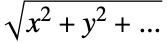 で正規化された
で正規化された 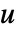 の勾配になる.
の勾配になる.
例題
すべて開くすべて閉じる例 (2)
左辺にNeumannValueが設定される.この方程式のデフォルトのノイマン境界被積分関数は ![]() である.
である.![]() ,の形式の境界被積分関数をモデル化するために,NeumannValue
,の形式の境界被積分関数をモデル化するために,NeumannValue ![]() が設定される:
が設定される:
スコープ (5)
非保存的物質移動のために,MassImpermeableBoundaryValueのような境界条件がNeumannBoundaryUnitNormalを生成することがある.非保存モデルのために不浸透性境界条件を設定する:
NeumannBoundaryUnitNormalをNIntegrateで使って境界を通過する流れが計算できる.単位Disk上のポアソン(Poisson)方程式を解く:
左にNeumannValueが設定される.この方程式についてのデフォルトのノイマン境界被積分関数は ![]() である.
である.![]() の形式の境界被積分関数をモデル化するために,NeumannValue
の形式の境界被積分関数をモデル化するために,NeumannValue ![]() が設定される:
が設定される:
NeumannValueの接線を作成する:
NeumannBoundaryUnitNormalのIndexed成分(![]() 成分)を使ってNeumannValueを計算する:
成分)を使ってNeumannValueを計算する:
アプリケーション (1)
AcousticRadiationValueはNeumannBoundaryUnitNormalを使って音の方向ベクトルを自動的に計算する.モデルパラメータ pars を使って周波数領域音圧場のモデル変数 vars を定義する:
特性と関係 (1)
境界単位法線は,領域上でポアソン方程式を解き,ディリクレ条件を0に指定することによって計算される.単位Disk上でポアソン方程式を計算する:
テキスト
Wolfram Research (2025), NeumannBoundaryUnitNormal, Wolfram言語関数, https://reference.wolfram.com/language/ref/NeumannBoundaryUnitNormal.html.
CMS
Wolfram Language. 2025. "NeumannBoundaryUnitNormal." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NeumannBoundaryUnitNormal.html.
APA
Wolfram Language. (2025). NeumannBoundaryUnitNormal. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NeumannBoundaryUnitNormal.html