

NormalMatrixQ
更多信息和选项

- 如果 m.ConjugateTranspose[m]ConjugateTranspose[m].m,则矩阵 m 是正规矩阵,这是实对称矩阵、厄米特矩阵、酉矩阵以及其他多种矩阵类型的推广. »
- 根据谱定理,正规矩阵 m 是最广义类型的可酉对角化矩阵,即存在某个酉矩阵
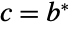 和对角矩阵
和对角矩阵 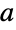 ,使得
,使得 ![m=u.d.TemplateBox[{u}, ConjugateTranspose] m=u.d.TemplateBox[{u}, ConjugateTranspose]](Files/NormalMatrixQ.zh/3.png) 成立 . »
成立 . » - NormalMatrixQ 适用于符号矩阵和数值矩阵.
- 可给出下列选项:
-
SameTest Automatic 测试表达式的相等关系的函数 Tolerance Automatic 近似数的容差 - 对于精确和符号矩阵,选项 SameTest->f 表明如果 f[aij,bij] 给出 True,则将两个元素 aij 和 bij 视为相等,其中 a=m.m 并且 b=m.m.
- 对于近似矩阵,选项 Tolerance->t 可用于表明满足 γ≤t γ∞ 的范数 γ=m.m-m.m∞ 被视为零,其中 γ∞ 是矩阵 m 的无穷范数.
范例
打开所有单元 关闭所有单元基本范例 (2)
范围 (10)
基本用法 (6)
特殊矩阵 (4)
选项 (2)
SameTest (1)
矩阵对于正实数 ![]() 是规范的,但是 NormalMatrixQ 给出 False:
是规范的,但是 NormalMatrixQ 给出 False:
使用选项 SameTest 以获取正确答案:
应用 (5)
正规矩阵是可酉对角化为 ![]() 的最广义矩阵类型,其中
的最广义矩阵类型,其中 ![]() 为对角矩阵,
为对角矩阵,![]() 为酉矩阵. 所有埃尔米特矩阵
为酉矩阵. 所有埃尔米特矩阵 ![]() 都是正规矩阵,因为等式两边都等于
都是正规矩阵,因为等式两边都等于 ![]() :
:
酉矩阵是正规矩阵,因为代入定义 ![]() 后,等式两边都会得到单位矩阵:
后,等式两边都会得到单位矩阵:
用 NormalMatrixQ 确认结果:
可以通过 EigenvalueDecomposition 将 ![]() 这样的正规矩阵酉对角化:
这样的正规矩阵酉对角化:
任意正规矩阵都可以用 ![]() 这种形式表示,据此,用一组给定的特征值生成正规矩阵,其中,
这种形式表示,据此,用一组给定的特征值生成正规矩阵,其中,![]() 为酉矩阵,
为酉矩阵,![]() 为对角矩阵:
为对角矩阵:
总的来说,该矩阵不是 Hermitian 矩阵,也不是反厄米特矩阵或酉矩阵:
如果用来生成矩阵的特征值是实数,则矩阵是Hermitian 矩阵:
因为正规矩阵可以酉对角化,所以计算矩阵函数特别简单. 如果 ![]() ,则
,则 ![]() ,可通过将
,可通过将 ![]() 应用于每个对角元素来计算
应用于每个对角元素来计算 ![]() . 考虑以下正规矩阵:
. 考虑以下正规矩阵:
计算 Eigensystem[n]:
计算 ![]() 并用 MatrixPower 确认:
并用 MatrixPower 确认:
计算 ![]() 并用 MatrixExp 确认:
并用 MatrixExp 确认:
计算 ![]() 并用 MatrixLog 确认:
并用 MatrixLog 确认:
计算 ![]() 并用 MatrixFunction 确认:
并用 MatrixFunction 确认:
许多矩阵分布可产生正态矩阵,包括 CircularRealMatrixDistribution:
CircularSymplecticMatrixDistribution:
GaussianOrthogonalMatrixDistribution:
GaussianUnitaryMatrixDistribution :
对于复正规矩阵,SchurDecomposition 总是等价于 Eigensystem:
属性和关系 (15)
NormalMatrixQ[m] 实际上等价于 m.mm.m:
当且仅当矩阵的 Hermitian 和反厄米特部分是可交换的,矩阵才是正规矩阵:
实际上,它总是可用 Eigensystem 酉对角化的:
对于正规矩阵 m,{s,j}=JordanDecomposition[m]:
可通过 UnitaryMatrixQ(设置 NormalizedFalse)快速进行验证:
对于正规矩阵,舒尔分解 {q,r} 与特征分解 {t,d} 其实是一样的:
计算 SchurDecomposition[n,RealBlockDiagonalFormFalse]:
为验证 ![]() 等于
等于 ![]() ,将每列的第一个元素设为 1. 以消除相位差异:
,将每列的第一个元素设为 1. 以消除相位差异:
用 HermitianMatrixQ 验证:
用 AntihermitianMatrixQ 验证:
用 UnitaryMatrixQ 验证:
相关指南
-
▪
- 矩阵判断
文本
Wolfram Research (2014),NormalMatrixQ,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NormalMatrixQ.html.
CMS
Wolfram 语言. 2014. "NormalMatrixQ." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/NormalMatrixQ.html.
APA
Wolfram 语言. (2014). NormalMatrixQ. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NormalMatrixQ.html 年
BibTeX
@misc{reference.wolfram_2025_normalmatrixq, author="Wolfram Research", title="{NormalMatrixQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/NormalMatrixQ.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_normalmatrixq, organization={Wolfram Research}, title={NormalMatrixQ}, year={2014}, url={https://reference.wolfram.com/language/ref/NormalMatrixQ.html}, note=[Accessed: 07-February-2026]}