Parallelogram
Parallelogram[p,{v1,v2}]
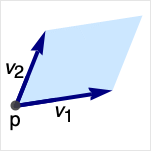
原点 p,方向 v1と v2の平行四辺形を表す.
詳細とオプション

- Parallelogramは,偏菱形および菱形としても知られる.
- Parallelogramは,
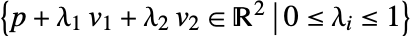 を表す.ただし,ベクトル viは,線形独立でなければならない.
を表す.ただし,ベクトル viは,線形独立でなければならない. - Parallelogram[]はParallelogram[{0,0},{{1,0},{1,1}}]に等しい.
- CanonicalizePolygonを使って平行四辺形を明示的なPolygonオブジェクトに変換することができる.
- Parallelogramは,幾何学的な領域およびグラフィックスプリミティブとして使われる.
- Parallelogramは,Graphicsで使える.
- グラフィックスでは,点 p とベクトル viがScaledおよびDynamicの式になり得る.
- グラフィックスの描画は,FaceForm,EdgeForm,Opacity,色等の指示子に影響される.
例題
すべて開くすべて閉じる例 (3)
スコープ (16)
グラフィックス (6)
アプリケーション (5)
特性と関係 (6)
Rectangleは,Parallelogramの特殊形である:
Polygonは,Parallelogramを一般化したものである:
Parallelepipedは,Parallelogramを任意次元に一般化する:
ImplicitRegionは,任意の平行四辺形を表すことができる:
ParametricRegionは,任意の平行四辺形を表すことができる:
Wolfram Research (2014), Parallelogram, Wolfram言語関数, https://reference.wolfram.com/language/ref/Parallelogram.html (2019年に更新).
テキスト
Wolfram Research (2014), Parallelogram, Wolfram言語関数, https://reference.wolfram.com/language/ref/Parallelogram.html (2019年に更新).
CMS
Wolfram Language. 2014. "Parallelogram." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Parallelogram.html.
APA
Wolfram Language. (2014). Parallelogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Parallelogram.html