Parallelogram
Parallelogram[p,{v1,v2}]
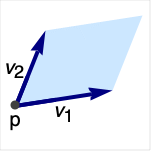
表示一个原点在 p、方向为 v1 和 v2 的平行四边形.
更多信息和选项

- Parallelogram 亦称为长菱形和菱形.
- Parallelogram 表示
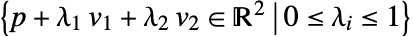 ,其中向量 vi 必须是线性独立的.
,其中向量 vi 必须是线性独立的. - Parallelogram[] 等价于 Parallelogram[{0,0},{{1,0},{1,1}}].
- CanonicalizePolygon 可用于把四边形转换成显式 Polygon 对象.
- Parallelogram 可被用作几何区域及图形基元.
- Parallelogram 可用在 Graphics 中.
- 在图形中,点 p 和向量 vi 可以是 Scaled 和 Dynamic 表达式.
- 有些指令,比如 FaceForm、EdgeForm、Opacity 和着色会影响图形渲染.
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (16)
图形 (6)
应用 (5)
和 Area 比较:
Parallelogram 可以平铺一个面:
属性和关系 (6)
Rectangle 是 Parallelogram 的特例:
Polygon 是 Parallelogram 的推广:
Parallelepiped 将 Parallelogram 推广至任意维度:
ImplicitRegion 可以表示任意平行四边形:
ParametricRegion 可以表示任意平行四边形:
Wolfram Research (2014),Parallelogram,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Parallelogram.html (更新于 2019 年).
文本
Wolfram Research (2014),Parallelogram,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Parallelogram.html (更新于 2019 年).
CMS
Wolfram 语言. 2014. "Parallelogram." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/Parallelogram.html.
APA
Wolfram 语言. (2014). Parallelogram. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Parallelogram.html 年