ProductDistribution
ProductDistribution[dist1,dist2,…]
表示独立分量分布为 dist1, dist2, … 的联合分布.
更多信息
- ProductDistribution[dist1,dist2,…] 的概率密度由
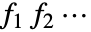 给出,其中 f1 是 dist1 的概率密度函数,f2 是 dist2 的概率密度函数等等.
给出,其中 f1 是 dist1 的概率密度函数,f2 是 dist2 的概率密度函数等等. - 符号 {disti,n} 表示 disti 重复 n 次.
- 分布 disti 可以是单变量、多变量、连续或离散分布的任意组合.
- ProductDistribution 可与 Mean、CDF 和 RandomVariate 等函数联合使用.
背景
- ProductDistribution[dist1,dist2,…,distn] 表示一个多变量统计分布,它的第
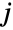 个边缘分布 (MarginalDistribution) 为 distj,并且各分量 dist1,dist2,…,distn 相互独立. 一个普通乘积分布 ProductDistribution[dist1,dist2,…,distn] 的概率密度函数 (PDF) 为
个边缘分布 (MarginalDistribution) 为 distj,并且各分量 dist1,dist2,…,distn 相互独立. 一个普通乘积分布 ProductDistribution[dist1,dist2,…,distn] 的概率密度函数 (PDF) 为 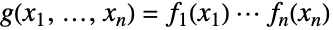 ,其中
,其中 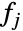 为 distj 的 PDF. 尽管所有的乘积分布都有这些属性,具体的乘积分布的特性和行为则由边缘分布 dist1,dist2,…,distn 所决定.
为 distj 的 PDF. 尽管所有的乘积分布都有这些属性,具体的乘积分布的特性和行为则由边缘分布 dist1,dist2,…,distn 所决定. - 乘积分布的各分量 dist1,dist2,…,distn 可以是连续或离散的,单变量或多变量的,可以由任意一个或所有有标准名称的分布(比如:BinomialDistribution、NormalDistribution、HypergeometricDistribution 等)以及它们的变体(通过 TransformedDistribution、CensoredDistribution、ProductDistribution、CopulaDistribution 等) 所组成. 而且,每个分量 distj 可以是符号式的(比如 NormalDistribution[μ,σ]),也可以是数值式的( 比如 NormalDistribution[0,1]),并且,可以用简写形式 ProductDistribution[{dist1,k1},{dist2,k2},… ,{distn,kn}] 来表示将第 j 个边缘分布 distj 重复 kj 次.
- 在二十世纪四十年代,有人提出了一个对乘积分布进行系统研究的项目. 尽管工作持续到了五十年代末,六十年代初,已接近尾声,但首次对此主题进行彻底详细讨论的是 Springer 和 Thompson 发表于1966年的一篇论文. 从那时起,研究方法不断被改进,使对特殊定义(如分段函数)的概率分布的乘积进行理论和算法上的研究成为可能,从实际运用的角度出发,乘积分布已被证明在机器学习和金融领域是极为重要的工具. 另外,人们还运用蒙特卡罗理论和其他数值法对乘积分布进行了深入研究.
- ProductDistribution 和其他各种分布之间存在着多种关系. ProductDistribution 是CopulaDistribution 的特例,因为 ProductDistribution[dist1,dist2,…,distn] 等价于 CopulaDistribution["Product",{dist1,dist2,…,distn}]. KDistribution 被定义为服从 GammaDistribution 的变数的乘积;两个 LogNormalDistribution 的乘积还是 LogNormalDistribution;BetaDistribution 和 GammaDistribution 的乘积为 GammaDistribution. 具有对角协方差矩阵的 MultinormalDistribution(同样还有 BinormalDistribution) 是 ProductDistribution(它的边缘分布为 NormalDistribution) 的一个例子.
范例
打开所有单元关闭所有单元范围 (26)
基本用途 (7)
参数分布 (6)
定义独立 PoissonDistribution 的乘积分布:
MultivariatePoissonDistribution 没有独立分量:
创建 StudentTDistribution 的两个独立例子的乘积分布:
求 MultinormalDistribution 的边缘:
是具有对角协方差矩阵的 MultinormalDistribution:
非参数分布 (3)
定义 SmoothKernelDistribution 的乘积:
从 中创建一个样本并为此定义一个 SmoothKernelDistribution:
定义一个 EmpiricalDistribution 的一个乘积:
定义 HistogramDistribution 的一个乘积分布:
导出分布 (10)
定义具有 CensoredDistribution 的乘积:
MarginalDistribution 选择 ProductDistribution 分量:
乘积分布的分量假设为是独立的,因此原分布不能恢复,当 ![]() 非零时:
非零时:
从 MixtureDistribution 中创建乘积分布:
求最小最大 OrderDistribution 的乘积分布:
定义 ParameterMixtureDistribution 的乘积分布:
乘积分布被用于 TransformedDistribution 的输入:
求 TransformedDistribution 的乘积分布:
求 TruncatedDistribution 的乘积分布:
求 TruncatedDistribution 的乘积分布:
两个 QuantityDistribution 的积的结果是 QuantityDistribution:
应用 (8)
两个人想要在下午5点到5点半之间于某地见面. 两人的到达时刻在该时间段上相互独立,并各自停留5分钟. 求两人能见面的概率:
均值的抽样分布由 NormalDistribution[0,1/10] 给出:
一种彩票销售10张票,每张票1美元. 每次只有一张彩票中奖. 一位赌徒只有5美元可以用于购买彩票. 求如果该赌徒购买5张属于5种不同类型的彩票时,他的中奖率:
在影院买票和买爆米花的等待时间是独立的,它们均是指数分布. 买票的平均等待时间是10分钟,买爆米花是5分钟. 求影迷就坐前等待小于25分钟的概率:
一个工厂生产的圆柱状滚子轴承. 轴承的直径是正态分布,均值为5厘米和标准偏差为0.01厘米. 轴承的长度是正态分布,均值为7厘米和标准偏差为0.01厘米. 假设直径和长度是独立分布的,求轴承的直径或长度不同于均值相差大于0.02厘米的概率.
属性和关系 (7)
文本
Wolfram Research (2010),ProductDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ProductDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2010. "ProductDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/ProductDistribution.html.
APA
Wolfram 语言. (2010). ProductDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ProductDistribution.html 年