MultivariatePoissonDistribution

MultivariatePoissonDistribution[μ0,{μ1,μ2,…}]

represents a multivariate Poisson distribution with mean vector {μ0+μ1,μ0+μ2,…}.

Details

  • The multivariate Poisson distribution corresponds to the distribution of {x0+x1,x0+x2,…}, where xi is Poisson distributed with mean μi.
  • The parameters μi can be any positive numbers.
  • MultivariatePoissonDistribution can be used with such functions as Mean, CDF, and RandomVariate.

Background & Context

  • MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}] represents a discrete multivariate statistical distribution supported over the subset of 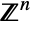, consisting of all tuples 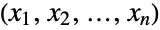of integers satisfying 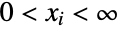and characterized by the property that each of the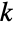 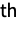^(th) (univariate) marginal distributions is a PoissonDistribution for 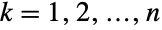. In other words, each of the variables 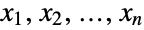satisfies xkPoissonDistribution[μ0+μk] for 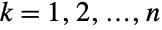. The multivariate Poisson distribution is parametrized by a positive real number μ0 and by a vector {μ1,μ2,…,μn} of real numbers, which together define the associated mean, variance, and covariance of the distribution. The multivariate Poisson distribution has a probability density function (PDF) that is discrete and unimodal.
  • Care must be exhibited to distinguish the multivariate Poisson distribution from the similarly named multiple Poisson distribution. The latter distribution became the focus of study in the late 1950s and is characterized by being a joint distribution of its univariate marginals. (In contrast, MultivariatePoissonDistribution is not a product of its univariate marginals.)
  • The study of the multivariate Poisson distribution began in the 1930s in the special case when 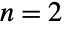(the so-called bivariate Poisson distribution), while analysis of the general multivariate case began in the late 1950s. Unlike other multivariate distributions such as the MultinormalDistribution, the multivariate Poisson distribution has been redefined several times, with many of its incarnations garnering mixed receptions and criticism from experts. In its most standard incarnation, the multivariate Poisson distribution (as implemented here) is considered to be the most natural multivariate extension of the univariate Poisson distribution and has found use as an alternative to hidden Markov models in the analysis and classification of neuronal spike patterns.
  • RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a multivariate Poisson distribution. Distributed[x,MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}]], written more concisely as xMultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}], can be used to assert that a random variable x is distributed according to a multivariate Poisson distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
  • The probability density and cumulative distribution functions for multivariate Poisson distributions may be given using PDF[MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}],{x1,x2,…,xn}] and CDF[MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}],{x1,x2,…,xn}]. The mean, median, variance, covariance, raw moments, and central moments may be computed using Mean, Median, Variance, Covariance, Moment, and CentralMoment, respectively.
  • DistributionFitTest can be used to test if a given dataset is consistent with a multivariate Poisson distribution, EstimatedDistribution to estimate a multivariate Poisson parametric distribution from given data, and FindDistributionParameters to fit data to a multivariate Poisson distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic multivariate Poisson distribution, and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic multivariate Poisson distribution.
  • TransformedDistribution can be used to represent a transformed multivariate Poisson distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a multivariate Poisson distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving multivariate Poisson distributions.
  • MultivariatePoissonDistribution is related to a number of other distributions. MultivariatePoissonDistribution is connected to PoissonDistribution, as discussed above, and while the one-dimensional marginal PDFs of MultivariatePoissonDistribution each satisfy a PoissonDistribution, each of the multivariate marginals is again an instance of MultivariatePoissonDistribution. MultivariatePoissonDistribution is a limiting case of MultinomialDistribution in a complicated but precise way, and because of its relation to the univariate PoissonDistribution, MultivariatePoissonDistribution is also related to BinomialDistribution, PolyaAeppliDistribution, and PoissonConsulDistribution.

Examples

open allclose all

Basic Examples  (4)

Probability mass function:

Cumulative distribution function:

Mean and variance:

Covariance matrix:

Scope  (8)

Generate a sample of pseudorandom vectors from a multivariate Poisson distribution:

Distribution parameters estimation:

Estimate the distribution parameters from sample data:

Goodness-of-fit test:

Skewness for each component depends on μ and mu_(i):

Kurtosis for each component depends on μ and mu_(i):

Correlation:

Different mixed moments for a bivariate Poisson distribution:

Mixed central moments:

Mixed factorial moments:

Mixed cumulants:

Closed form for a symbolic order:

Hazard function:

Marginal distributions:

Applications  (2)

In clinical studies, medicine A on average caused an adverse reaction in 12 people per 100000 and medicine B in 9 people per 100000. It has also been determined that while some people will show no adverse reaction to medicine A or B alone, the combination of both caused an adverse reaction on average in 1 person per 500000. Assuming a Poisson model, find the adverse reaction distribution in the population of 10000:

Find the probability that there are at most 3 adverse reactions to medicine A and at most 4 adverse reactions to medicine B:

A university campus lies completely within twin cities A and B. On a given day there are, on average, 10 car accidents on campus; outside of campus there are 5 more in city A and 10 more in city B. Find the joint distribution of the number of accidents in the twin cities:

Probability density function:

Find the average number of accidents in each city:

Find the average total number of accidents in the twin cities:

Find the probability that on a given day there are more accidents in city A than in city B:

Use a random sample to find the probability that there are at least 12 accidents per day in the twin cities:

Properties & Relations  (4)

Multivariate Poisson distribution is closed under addition:

One-dimensional multivariate Poisson distribution is a PoissonDistribution:

The components are correlated for all allowed values of parameters:

Multivariate Poisson cannot be represented as a product of its marginal distributions:

Find marginal distributions:

Find ProductDistribution of marginal distributions:

Compare covariance matrices:

Compare PDFs:

Wolfram Research (2010), MultivariatePoissonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html.

Text

Wolfram Research (2010), MultivariatePoissonDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html.

CMS

Wolfram Language. 2010. "MultivariatePoissonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html.

APA

Wolfram Language. (2010). MultivariatePoissonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html

BibTeX

@misc{reference.wolfram_2024_multivariatepoissondistribution, author="Wolfram Research", title="{MultivariatePoissonDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multivariatepoissondistribution, organization={Wolfram Research}, title={MultivariatePoissonDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html}, note=[Accessed: 30-December-2024 ]}