RadonTransform
RadonTransform[expr,{x,y},{p,ϕ}]
给出 expr 的拉东变换.
更多信息和选项

- 函数
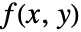 的拉东变换被定义为
的拉东变换被定义为 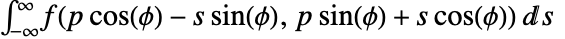 .
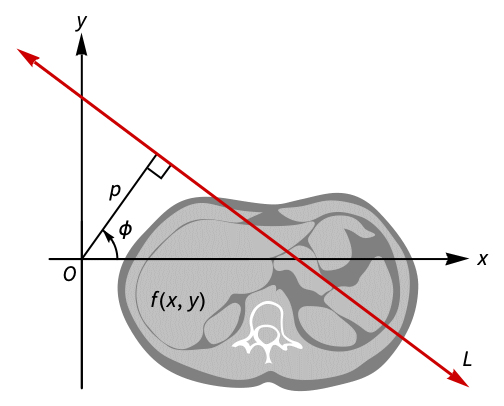
. - 从几何学上来说,拉东变换表示
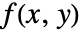 沿直线
沿直线 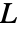 的积分,直线的法线形式由方程
的积分,直线的法线形式由方程 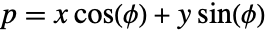 给出,其中 -∞<p<∞ 和 -π/2<ϕ<π/2.
给出,其中 -∞<p<∞ 和 -π/2<ϕ<π/2. - 可以给出下列选项:
-
Assumptions $Assumptions 对参数的假设 GenerateConditions False 是否给出涉及参数条件的结果 Method Automatic 使用什么方法 - 在 TraditionalForm 中,用
![TemplateBox[{{f, (, {x, ,, y}, )}, x, y, p, phi}, RadonTransform] TemplateBox[{{f, (, {x, ,, y}, )}, x, y, p, phi}, RadonTransform]](Files/RadonTransform.zh/7.png) 输出 RadonTransform.
输出 RadonTransform.
范例
打开所有单元关闭所有单元范围 (10)标准用法实例范围调查
高斯函数 (5)
分段和广义函数 (3)
应用 (2)用该函数可以解决的问题范例
属性和关系 (10)函数的属性及与其他函数的关联
用 Integrate 获取同样的结果:
RadonTransform 和 InverseRadonTransform 互为逆:
RadonTransform 是线性运算符:
RadonTransform 的移位属性:
RadonTransform 的对称属性:
RadonTransform 的齐次性:
RadonTransform 的缩放属性:
导数的 RadonTransform:
可以用傅立叶变换来计算 RadonTransform:
直接用 RadonTransform 获取同样的结果:
Wolfram Research (2017),RadonTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RadonTransform.html.
文本
Wolfram Research (2017),RadonTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RadonTransform.html.
CMS
Wolfram 语言. 2017. "RadonTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RadonTransform.html.
APA
Wolfram 语言. (2017). RadonTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RadonTransform.html 年