WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

RegionFarthestDistance[reg1,reg2]

領域 reg1と領域 reg2にある点の間の最遠距離を与える．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
特殊領域  
数式定義領域  
メッシュ領域  
派生領域  
地理領域  
オプション  
WorkingPrecision  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

RegionFarthestDistance

RegionFarthestDistance[reg1,reg2]

領域 reg1と領域 reg2にある点の間の最遠距離を与える．

詳細とオプション

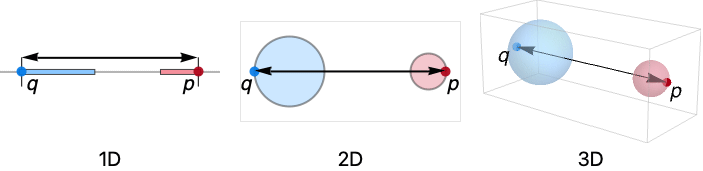
  • RegionFarthestDistanceは，最大領域距離およびスパン距離としても知られている．
  • 最大距離は，2つの領域の点がどれくらい離れているかを測定する．
  • RegionFarthestDistanceはある領域内の点から他の領域内のすべての点までの距離の最大のものである．
  • 点 p と点 q の間の距離はNorm[p-q]であると見なされる．
  • RegionFarthestDistanceは，事実上，MaxValue[Norm[p-q],{p∈reg1,q∈reg2}]で与えられる．
  • 領域が閉じていない限り最遠距離は領域内の点では達成されないが，領域の閉鎖で達成される場合がある．

例題

すべて開く すべて閉じる

例  (3)

ある点から単位円板までの最大距離を求める：

Wolfram Language code: RegionFarthestDistance[Disk[], {3, 3}]

距離を位置の関数としてプロットする：

Wolfram Language code: Plot3D[RegionFarthestDistance[Disk[], {x, y}], {x, -2, 2}, {y, -2, 2}]

円板と矩形の間の最大距離を求める：

Wolfram Language code: RegionFarthestDistance[Disk[], Rectangle[]]

領域を表示する：

Wolfram Language code: Graphics[{Opacity[1 / 3], Disk[], Rectangle[]}, Axes -> True]

2つのメッシュ間の最大距離を求める：

Wolfram Language code: Subscript[ℛ, 1] = ResourceData["Stanford Bunny"]; Subscript[ℛ, 2] = TransformedRegion[ResourceData["Stanford Dragon"], TranslationTransform[{0.15, 0, 0}]];
Wolfram Language code: RegionFarthestDistance[Subscript[ℛ, 1], Subscript[ℛ, 2]]

メッシュを表示する：

Wolfram Language code: Show[Subscript[ℛ, 1], HighlightMesh[Subscript[ℛ, 2], {Style[1, None], 2}]]

スコープ  (16)

特殊領域  (8)

点：

Wolfram Language code: RegionFarthestDistance[Point[{{1, 1}, {1, 2}}], Point[{3, 4}]]

RegionFarthestDistanceには座標のリストが使える：

Wolfram Language code: RegionFarthestDistance[{{1, 1}, {1, 2}}, {3, 4}]

線：

Wolfram Language code: RegionFarthestDistance[Line[{{0, 0}, {1, 1}, {2, -1}}], Line[{{-1, 1}, {2, 0}}]]
Wolfram Language code: RegionFarthestDistance[Line[{{0, -1, 2}, {2, -1, -3}}], Line[{{-1, 1, 3}, {2, -1, 0}}]]

多角形：

Wolfram Language code: RegionFarthestDistance[Polygon[{{0, 0}, {2, 1}, {1, 3}}], Polygon[{{2, 0}, {0, 3}, {-1, 1}}]]
Wolfram Language code: RegionFarthestDistance[Triangle[], Rectangle[]]

シンプレックス：

Wolfram Language code: RegionFarthestDistance[Simplex[{{0}, {1}}], Simplex[{{2}, {3}}]]
Wolfram Language code: RegionFarthestDistance[Simplex[{{0, 0}, {2, 0}, {0, 2}}], Simplex[{{1, -1}, {1, 1}, {2, -1}}]]
Wolfram Language code: RegionFarthestDistance[Simplex[{{0, 0, 0}, {2, 0, 0}, {0, 2, 0}, {0, 0, 2}}], Simplex[{{-1, 0, 1}, {2, 0, 1}, {3, 2, 0}, {2, 0, 2}}]]

ボックス：

Wolfram Language code: RegionFarthestDistance[Rectangle[], Rectangle[{2, 1}]]
Wolfram Language code: RegionFarthestDistance[Cuboid[], Cuboid[{3, 2, 1}]]
Wolfram Language code: RegionFarthestDistance[Cube[], Cube[2]]

球体：

Wolfram Language code: RegionFarthestDistance[Disk[], Disk[{1, 1}]]
Wolfram Language code: RegionFarthestDistance[Ball[], Ball[{1, 2, 3}]]

球：

Wolfram Language code: RegionFarthestDistance[Circle[], Circle[{1, 2}]]
Wolfram Language code: RegionFarthestDistance[Sphere[], Sphere[{4, 5, 6}]]

n内の領域：

Wolfram Language code: RegionFarthestDistance[Simplex[{{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}], {1, 2, 3, 4}]
Wolfram Language code: RegionFarthestDistance[Point[{1, 2, 3, 4, 5}], {6, 7, 8, 9, 10}]
Wolfram Language code: RegionFarthestDistance[Cuboid[{1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}], {11, 12, 13, 14, 15}]
Wolfram Language code: RegionFarthestDistance[Ball[{1, 2, 3, 4, 5, 6, 7}, 8], {9, 10, 11, 12, 13, 14, 15}]

数式定義領域  (2)

ImplicitRegionとして表された円板までの距離：

Wolfram Language code: ℛ = ImplicitRegion[x^2 + y^2 ≤ 1, {x, y}];
Wolfram Language code: RegionPlot[ℛ]
Wolfram Language code: RegionFarthestDistance[ℛ, {4, 0}]

円柱：

Wolfram Language code: ℛ = ImplicitRegion[x^2 + y^2 ≤ 1, {x, y, {z, -3, 3}}];
Wolfram Language code: RegionFarthestDistance[ℛ, {3, 0, 0}]

ParametricRegionとして表された円板までの距離：

Wolfram Language code: ℛ = ParametricRegion[{r Cos[θ], r Sin[θ]}, {{r, 0, 1}, {θ, 0, 2π}}];
Wolfram Language code: RegionFarthestDistance[ℛ, {4, 0}]

円板の有理パラメータ化を使う：

Wolfram Language code: ℛ = ParametricRegion[{r(1 - t^2/1 + t^2), r(2t/1 + t^2)}, {t, {r, -1, 1}}];
Wolfram Language code: RegionFarthestDistance[ℛ, {3, 0}]

円柱：

Wolfram Language code: ℛ = ParametricRegion[{r Cos[θ], r Sin[θ], z}, {{r, 0, 1}, {θ, 0, 2π}, {z, -3, 3}}];
Wolfram Language code: RegionFarthestDistance[ℛ, {3, 0, 0}]

メッシュ領域  (1)

2つの1Dメッシュ間の最長距離：

Wolfram Language code: Subscript[ℛ, 1] = ConvexHullMesh[RandomReal[{-1, 0}, {10, 1}]]; Subscript[ℛ, 2] = ConvexHullMesh[RandomReal[1, {10, 1}]];
Wolfram Language code: Show[Subscript[ℛ, 1], HighlightMesh[Subscript[ℛ, 2], {Style[0, None], 1}], PlotRange -> 1]
Wolfram Language code: RegionFarthestDistance[Subscript[ℛ, 1], Subscript[ℛ, 2]]

2D：

Wolfram Language code: Subscript[ℛ, 1] = ConvexHullMesh[RandomReal[1, {10, 2}]]; Subscript[ℛ, 2] = ConvexHullMesh[RandomReal[{1 / 2, 3 / 2}, {10, 2}]];
Wolfram Language code: Show[Subscript[ℛ, 1], HighlightMesh[Subscript[ℛ, 2], 2]]
Wolfram Language code: RegionFarthestDistance[Subscript[ℛ, 1], Subscript[ℛ, 2]]

3D：

Wolfram Language code: Subscript[ℛ, 1] = ConvexHullMesh[RandomReal[1, {20, 3}]]; Subscript[ℛ, 2] = ConvexHullMesh[RandomReal[{3 / 4, 3 / 2}, {20, 3}]];
Wolfram Language code: Show[Subscript[ℛ, 1], HighlightMesh[Subscript[ℛ, 2], {Style[1, None], 2}]]
Wolfram Language code: RegionFarthestDistance[Subscript[ℛ, 1], Subscript[ℛ, 2]]

派生領域  (2)

RegionIntersectionまでの距離：

Wolfram Language code: ℛ = RegionIntersection[Disk[{0, 0}, 1], Disk[{0, 1}, 1]];
Wolfram Language code: RegionFarthestDistance[ℛ, {1, 1}]
Wolfram Language code: Show[Graphics[{Red, Point[{1, 1}]}], RegionPlot[ℛ]]

TransformedRegionまでの距離：

Wolfram Language code: ℛ = TransformedRegion[Disk[], ScalingTransform[{3, 2}]];
Wolfram Language code: RegionFarthestDistance[ℛ, {4, 3}]
Wolfram Language code: Show[DiscretizeRegion[ℛ, {{-3, 3}, {-2, 2}}], Graphics[{Red, Point[{4, 3}]}]]

地理領域  (3)

GeoPositionによる多角形間の距離：

Wolfram Language code: Subscript[ℛ, 1] = Polygon[GeoPosition[«1»]]; Subscript[ℛ, 2] = Polygon[GeoPosition[{{{45.9224464031654, 7.04419957737879}, {45.9225460115502, 7.04438238453911}, {45.9224654000104, 7.04450778935277}, {45.9133509165998, 7.06078795724687}, {45.9002287665667, 7.06418987722783}, {45.8952319956228, 7.07659165871427} ... 403, 8.22363969999999}, {39.1875155, 8.30962040000001}, {39.1443383, 8.3171627}}, {{36.7984641, 12.051308}, {36.7548795, 12.052027}, {36.7350588, 12.0043979}, {36.7680342, 11.956884}, {36.8163251, 11.9258571}, {36.839047, 11.9606946}}}]];
Wolfram Language code: RegionFarthestDistance[Subscript[ℛ, 1], Subscript[ℛ, 2]]

GeoGridPositionによる多角形間の距離：

Wolfram Language code: Subscript[ℛ, 1] = Polygon[GeoGridPosition[«2»]]; Subscript[ℛ, 2] = Polygon[GeoGridPosition[{{{7.04419957737879, 51.814195868999875}, {7.04438238453911, 51.81433906045609}, {7.04450778935277, 51.814223177784484}, {7.06078795724687, 51.801121788354756}, {7.06418987722783, 51.782263455595206}, {7.07659165871427, 51.7 ... 0141598803586}}, {{12.051308, 39.62515779284907}, {12.052027, 39.57074337120453}, {12.0043979, 39.54600788730125}, {11.956884, 39.587163467595836}, {11.9258571, 39.64746580472894}, {11.960694600000002, 39.675852502801604}}}, "Mercator"]];
Wolfram Language code: RegionFarthestDistance[Subscript[ℛ, 1], Subscript[ℛ, 2]]

RegionFarthestDistanceは地理実体を持つ多角形に使うことができる：

Wolfram Language code: Subscript[ℛ, 1] = Polygon[Entity["Country", "UnitedKingdom"]]; Subscript[ℛ, 2] = Polygon[Entity["Country", "Italy"]];
Wolfram Language code: RegionFarthestDistance[Subscript[ℛ, 1], Subscript[ℛ, 2]]

オプション  (2)

WorkingPrecision  (2)

RegionFarthestDistanceは入力と同じ精度で距離を計算しようとする：

Wolfram Language code: RegionFarthestDistance[Disk[], Point[{4, 4}]]

機械演算で距離を計算する：

Wolfram Language code: RegionFarthestDistance[Disk[], Point[{4, 4}], WorkingPrecision -> MachinePrecision]

場合によっては厳密な答が計算できないことがある：

Wolfram Language code: RegionFarthestDistance[ImplicitRegion[x ^ 6 + y ^ 6 - x y <= 1, {x, y}], Point[{2, 3}]]

30桁精度でRegionFarthestDistanceを求める：

Wolfram Language code: RegionFarthestDistance[Disk[], Point[{4, 4}], WorkingPrecision -> 30]

特性と関係  (4)

FullRegionと非空の領域間の最大距離はInfinityである：

Wolfram Language code: RegionFarthestDistance[FullRegion[2], {0, 0}]

EmptyRegionまでの最大距離は負のInfinityである：

Wolfram Language code: RegionFarthestDistance[EmptyRegion[2], {0, 0}]

2点間の最遠距離はEuclideanDistanceに等しい：

Wolfram Language code: RegionFarthestDistance[{1, 2}, {3, 4}]
Wolfram Language code: EuclideanDistance[{1, 2}, {3, 4}]

2つの点集合間の最遠距離は任意の２点間の最大EuclideanDistanceである：

Wolfram Language code: 𝒜 = {{0, 0}, {1, 2}, {4, 3}}; ℬ = {{4, 2}, {3, 0}};
Wolfram Language code: RegionFarthestDistance[𝒜, ℬ] === Max[Table[EuclideanDistance[a, b], {a, 𝒜}, {b, ℬ}]]

ある領域とある単一の点の間の最遠距離はRegionHausdorffDistanceに等しい：

Wolfram Language code: RegionFarthestDistance[Disk[], Point[{3, 5}]] === RegionHausdorffDistance[Disk[], Point[{3, 5}]]
Wolfram Research (2023), RegionFarthestDistance, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionFarthestDistance.html.

テキスト

Wolfram Research (2023), RegionFarthestDistance, Wolfram言語関数， https://reference.wolfram.com/language/ref/RegionFarthestDistance.html.

CMS

Wolfram Language. 2023. "RegionFarthestDistance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RegionFarthestDistance.html.

APA

Wolfram Language. (2023). RegionFarthestDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegionFarthestDistance.html

BibTeX

@misc{reference.wolfram_2026_regionfarthestdistance, author="Wolfram Research", title="{RegionFarthestDistance}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/RegionFarthestDistance.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_regionfarthestdistance, organization={Wolfram Research}, title={RegionFarthestDistance}, year={2023}, url={https://reference.wolfram.com/language/ref/RegionFarthestDistance.html}, note=[Accessed: 03-November-2026]}