SignedRegionDistance[reg,p]
gives the minimum distance from the point p to the region reg if p is outside the region and the minimum distance to the complement of reg if p is inside the region.
SignedRegionDistance[reg]
gives a RegionDistanceFunction[…] that can be applied repeatedly to different points.


SignedRegionDistance
SignedRegionDistance[reg,p]
gives the minimum distance from the point p to the region reg if p is outside the region and the minimum distance to the complement of reg if p is inside the region.
SignedRegionDistance[reg]
gives a RegionDistanceFunction[…] that can be applied repeatedly to different points.
Details and Options

- SignedRegionDistance is also known as signed distance function and signed distance transform.
- SignedRegionDistance is positive for points outside the region and negative for points inside the region. The absolute value measures how close the point is to the boundary.
- The distance between points q and p is taken to be Norm[p-q].
- SignedRegionDistance is effectively MinValue[{Norm[p-q],q∈reg},q∈reg] when p is not in reg and -MinValue[{Norm[p-q],q∉reg},q] otherwise.
- SignedRegionDistance can be used with symbolic regions and points in GeometricScene.
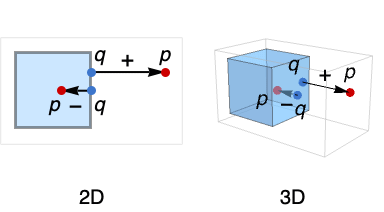
Examples
open all close allBasic Examples (2)
Find the signed distance from a point inside to the unit disk:
Plot the distance as a function of position:
Find the signed distance from a point to a MeshRegion:
With one argument, you get a RegionDistanceFunction:
Scope (17)
Special Regions (8)
The signed distance to a Point is always non-negative, as it has no interior:
Plot the signed distance from a three-point set:
The signed distance to a Line can be negative in 1D:
But in 2D and above, it is always non-negative:
Plot the signed distance from a line in 2D:
The signed distance from a Cuboid can be negative in any dimension:
Plot the signed distance to a rectangle:
The signed distance from a full-dimensional Simplex can be negative:
But the signed distance to a lower-dimensional simplex cannot:
Plot the signed distance to a 2D simplex:
The signed distance to a Disk can be negative:
Ball generalizes Disk to any dimension:
Plot the signed distance to a disk:
The signed distance to an Ellipsoid can be negative in any dimension:
Plot the signed distance to an ellipsoid in 2D:
The distance to a Circle is always non-negative, as it has no interior:
The same goes for Sphere in any dimension:
Plot the signed distance to a circle:
Cone:
Formula Regions (2)
The signed distance to a disk represented as an ImplicitRegion:
The distance to a disk represented as a ParametricRegion:
Mesh Regions (4)
The signed distance to a BoundaryMeshRegion can be negative in any dimension:
Signed distance cannot be negative to a 0D MeshRegion in 1D:
But it can for a 1D MeshRegion:
Signed distance cannot be negative to a 0D MeshRegion in 2D:
Nor for a 1D MeshRegion:
But it can for a 2D MeshRegion:
Signed distance cannot be negative to a 0D MeshRegion in 3D:
Nor for a 1D MeshRegion:
Nor for a 2D MeshRegion:
But it can for a 3D MeshRegion:
Derived Regions (3)
The signed distance to a RegionIntersection:
The signed distance to a TransformedRegion:
The signed distance to a RegionBoundary is always non-negative:
Applications (2)
If ![]() is a region that is full-dimensional, then the depth of a point
is a region that is full-dimensional, then the depth of a point ![]() is the negative signed region distance. Find the depth of {1,1} in Disk[{0,0},5]:
is the negative signed region distance. Find the depth of {1,1} in Disk[{0,0},5]:
To illustrate it, you need to compute the nearest point in ![]() :
:
Find the depth of the point {1,1,1} in Cuboid[{0,0,0},{2,2,2}]:
To illustrate it, you need to compute the nearest point in ![]() :
:
Properties & Relations (5)
A point is a RegionMember if the signed distance to the region is non-positive:
A point on the RegionBoundary has signed distance 0:
A point is in the interior of the region if the signed distance to the region is negative:
Abs of SignedRegionDistance is the MinValue of the distance to the RegionBoundary:
For a point outside the region, RegionDistance and SignedRegionDistance are the same:
Related Guides
History
Text
Wolfram Research (2014), SignedRegionDistance, Wolfram Language function, https://reference.wolfram.com/language/ref/SignedRegionDistance.html.
CMS
Wolfram Language. 2014. "SignedRegionDistance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SignedRegionDistance.html.
APA
Wolfram Language. (2014). SignedRegionDistance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SignedRegionDistance.html
BibTeX
@misc{reference.wolfram_2025_signedregiondistance, author="Wolfram Research", title="{SignedRegionDistance}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SignedRegionDistance.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_signedregiondistance, organization={Wolfram Research}, title={SignedRegionDistance}, year={2014}, url={https://reference.wolfram.com/language/ref/SignedRegionDistance.html}, note=[Accessed: 25-February-2026]}