RegionFarthestDistance
RegionFarthestDistance[reg1,reg2]
给出区域 reg1 和 reg2 中的点之间最远的距离.
更多信息和选项

- RegionFarthestDistance 亦称为最大区域距离和跨距.
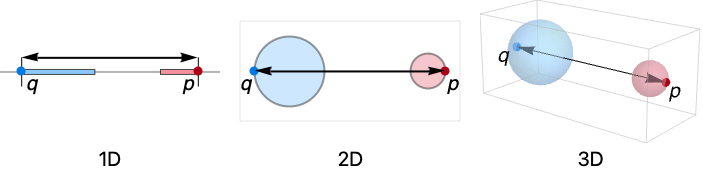
- 最远距离衡量两个区域的点相距多远.
- RegionFarthestDistance 是从一个区域中的一个点到另一个区域中的所有点的所有距离中的最大值.
- 点 p 和 q 之间的距离为 Norm[p-q].
- 实际上 RegionFarthestDistance 由 MaxValue[Norm[p-q],{p∈reg1,q∈reg2}] 给出.
- 除非区域是闭合的,否则最远距离可能不是通过区域中的点而是通过区域的闭包获得的.
范例
打开所有单元关闭所有单元范围 (16)
特殊区域 (8)
公式区域 (2)
导出区域 (2)
地理区域 (3)
选项 (2)
WorkingPrecision (2)
RegionFarthestDistance 将尝试使用与输入相同的精度来计算距离:ts:
用 30 位精度求 RegionFarthestDistance:
属性和关系 (4)
FullRegion 和非空区域之间的最远距离是 Infinity:
到 EmptyRegion 的最远距离是负 Infinity:
两点之间的最远距离等价于 EuclideanDistance:
两个点集之间的最远距离是任意两点之间最大的 EuclideanDistance:
区域与一个点之间的最远距离等价于 RegionHausdorffDistance:
文本
Wolfram Research (2023),RegionFarthestDistance,Wolfram 语言函数,https://reference.wolfram.com/language/ref/RegionFarthestDistance.html.
CMS
Wolfram 语言. 2023. "RegionFarthestDistance." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RegionFarthestDistance.html.
APA
Wolfram 语言. (2023). RegionFarthestDistance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RegionFarthestDistance.html 年