RiemannSiegelZ

RiemannSiegelZ[t]

リーマン・ジーゲル(Riemann–Siegel)関数 TemplateBox[{t}, RiemannSiegelZ]与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • TemplateBox[{t}, RiemannSiegelZ]=ⅇ^(ⅈ TemplateBox[{t}, RiemannSiegelTheta])TemplateBox[{{{1, /, 2}, +, {ⅈ, , t}}}, Zeta]，ただし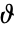， はリーマン・ジーゲルのゼータ関数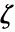， はリーマンのゼータ関数とする．
  • 実数 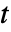について，|TemplateBox[{t}, RiemannSiegelZ]|=|TemplateBox[{{{1, /, 2}, +, {ⅈ, , t}}}, Zeta]|が成立する．
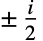  • TemplateBox[{t}, RiemannSiegelZ]は，虚軸上のから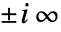の分枝切断線を除いて 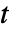の解析的な関数となる．
  • 特別な引数の場合，RiemannSiegelZは，自動的に厳密値を計算する．
  • RiemannSiegelZは任意の数値精度で評価できる．
  • RiemannSiegelZは自動的にリストに縫い込まれる．
  • RiemannSiegelZは，IntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (6)

数値的に評価する：

数値根を求める：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

原点における級数展開：

特異点における級数展開：

スコープ  (27)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率的に評価する：

RiemannSiegelZは，IntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のRiemannSiegelZ関数を計算することもできる：

特定の値  (2)

ゼロにおける値：

RiemannSiegelZ[x]の最初の正の最大値を求める：

可視化  (3)

RiemannSiegelZをプロットする：

RiemannSiegelZ関数の実部をプロットする：

RiemannSiegelZ関数の虚部をプロットする：

RiemannSiegelZ関数の実部をプロットする：

RiemannSiegelZ関数の虚部をプロットする：

関数の特性  (11)

RiemannSiegelZはすべての実数値について定義される：

複素領域：

RiemannSiegelZは恒等式を介して定義される：

RiemannSiegelZは要素単位でリストに縫い込まれる：

RiemannSiegelZは x の解析関数である：

RiemannSiegelZは非増加でも非減少でもない：

RiemannSiegelZは単射ではない：

RiemannSiegelZは非負でも非正でもない：

RiemannSiegelZは特異点も不連続点も持たない：

RiemannSiegelZは凸でも凹でもない：

TraditionalFormによる表示：

微分  (3)

についての一次導関数：

導関数を数値的に評価する：

についての一次および二次の導関数：

についての一次および二次の導関数をプロットする：

級数展開  (2)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

生成点におけるテイラー展開：

アプリケーション  (6)

複素平面上で実部と虚部をプロットする：

虚軸に沿った分枝切断線上で見る：

FindRootを使ってRiemannSiegelZの零点を求める：

あるいはZetaZeroを使ってみる：

零点をいくつか求める：

RiemannSiegelZの消えていく実部と虚部の曲線をプロットする：

リーマン仮説のあるバージョンによると の極限 が消えなければならない：

積分の値を両対数的にプロットする：

臨界線に沿ったリーマンゼータ関数の「信号パワー」を計算する：

漸近的な値との差分をプロットする：

Sin[RiemannSiegelTheta[t]]とRiemannSiegelZ[t]の根のインターレースを示す：

特性と関係  (2)

リーマンゼータ関数との関係：

超越方程式の根を数値的に求める：

考えられる問題  (2)

$MaxExtraPrecisionの設定値を大きくする必要があるかもしれない：

機械数の入力で高精度の結果が得られることがある：

おもしろい例題  (3)

RiemannSiegelZの回帰プロット：

RiemannSiegelZ を音として演奏する：

RiemannSiegelZをアニメーションにする：

Wolfram Research (1991), RiemannSiegelZ, Wolfram言語関数， https://reference.wolfram.com/language/ref/RiemannSiegelZ.html （2023年に更新）.

テキスト

Wolfram Research (1991), RiemannSiegelZ, Wolfram言語関数， https://reference.wolfram.com/language/ref/RiemannSiegelZ.html （2023年に更新）.

CMS

Wolfram Language. 1991. "RiemannSiegelZ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/RiemannSiegelZ.html.

APA

Wolfram Language. (1991). RiemannSiegelZ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RiemannSiegelZ.html

BibTeX

@misc{reference.wolfram_2024_riemannsiegelz, author="Wolfram Research", title="{RiemannSiegelZ}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/RiemannSiegelZ.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_riemannsiegelz, organization={Wolfram Research}, title={RiemannSiegelZ}, year={2023}, url={https://reference.wolfram.com/language/ref/RiemannSiegelZ.html}, note=[Accessed: 22-November-2024 ]}