RiskReductionImportance

RiskReductionImportance[rdist,t]

ReliabilityDistribution rdist の全成分の時間 t におけるリスク低減重要度を与える．

RiskReductionImportance[fdist,t]

FailureDistribution fdist の全成分の時間 t におけるリスク低減重要度を与える．

詳細

  • RiskReductionImportanceはリスク低減価値としても知られている．
  • 成分 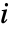のリスク低減重要度は，成分 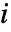が完全だった場合に系の不信頼性が低下する因子である．つまり，これは，成分 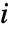を向上させることで系の信頼性が増す可能性を示す．
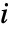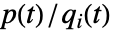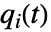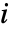  • 時間 t における成分 のリスク低減重要度は で与えられる．ただし，は 番目の成分が絶対に故障しなかった場合に系が故障した確率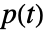，は系が故障した確率である．
  • 結果は rdist または fdist における分布リストの成分順で返される．

例題

すべて開くすべて閉じる

例  (3)

異なる寿命分布を持ち，直列接続された2つの成分：

結果はReliabilityDistributionにおける分布リストと同じ順で返される：

並列成分を改善することで系の信頼性を無限に向上させることができる：

故障の木に基づいたモデリングを使って系を定義する：

スコープ  (19)

ReliabilityDistributionモデル  (10)

同じ寿命分布を持ち，並列接続された2つの成分：

重要度は等しい：

同じ寿命分布を持ち，直列接続された2つの成分：

重要度は等しい：

動くためには寿命分布の等しい3つの成分のうち2つが必要な系：

重要度は等しい：

寿命分布が等しい単純な混合系：

重要度を計算する：

成分 が最も重要であり， と はその対称性のゆえに同等に重要である：

ある成分と並列に接続された直列接続の系：

重要度を計算する：

成分 が最も重要だが，無限大と等しいためプロットには示されていない：

単純な混合系でパラメータの変化が与える影響を調べる：

重要度を計算する：

並列成分の一つである を悪化させた場合の重要度の変化を示す：

分布が異なる他の2つの成分と並列に接続された1つの成分：

時間の特定の1点における重要性尺度を厳密な結果として求める：

機械精度での結果：

記号式としての結果：

任意の有効なReliabilityDistributionを使うことができる：

より信頼性の低い がより重要である：

ReliabilityDistributionは異なる分布族を含むことができる：

部分系の重要度尺度を得るために段階を追って系をモデル化する：

重要度を時間に沿ってプロットする：

FailureDistributionモデル  (9)

2つの基本事象のどちらもが頂上事象に繋がる：

重要度は等しい：

基本事象の両方がともに起った場合にのみ頂上事象に繋がる：

重要度は等しい：

基本事象の分布が等しいボーティングゲート：

重要度は等しい：

AndゲートとOrゲートの両方がある単純な系：

基本事象 が最も重要である：

と はその対称性のゆえに同等に重要である：

AndゲートとOrゲートの両方がある単純な系：

重要度を示す：

単純な混合系におけるパラメータ変更の影響を調べる：

重要度を計算する：

基本事象の一つ を悪化させた場合の重要度の変化を示す：

任意の有効なFailureDistributionを使うことができる：

より信頼性の低い がより重要である：

FailureDistributionは異なる分布族を含むことができる：

部分系の重要度尺度を得るために段階を追って系をモデル化する：

重要度を時間に沿ってプロットする：

アプリケーション  (3)

航空機の離陸の際の信頼性を高める可能性が最も高いのはどの成分かを分析する．格納扉は自動・手動のどちらで開くこともできる：

2つの燃料ポンプを動かすためには動力が必要である：

さらに2つのポンプを信頼できる電池を使って動かすことができる．したがって次の燃料移送構造となる：

航空機の除氷装置と燃料の収蔵タンクも必要である：

寿命分布を定義する：

重要度を計算する：

最初のうちは動力の改善が信頼性を高める．しかし，長い目で見るといろいろなポンプの改善が信頼性の向上に繋がる：

作業時間が3時間の系で，どの成分を改善することが最も適切であるかを求める：

時間に沿って信頼性を示す：

作業時間が3時間だと仮定すると，成分 が系の信頼性を改善するのに最も役に立つ：

重要性は を改善することによって系の不信頼性が低減される因子である：

弁が1つで余分なポンプが2つ付いた揚水装置を考える．成分の信頼性は確率で与えられる：

系の信頼性を改善するのに最も役立つ成分はどれかを求める：

特性と関係  (5)

RiskReductionImportanceはProbabilityによって定義することができる：

系の基本的な不信頼性を計算する：

成分が常に動いている場合の不信頼性：

基本的な不信頼性と常に動いている成分の不信頼性の比率：

定義と比較する：

RiskReductionImportanceはCriticalityFailureImportanceに関連している：

リスク低減重要性を計算する：

定義と比較する：

すべての成分が並列の系のRiskReductionImportanceはである：

ではないすべての重要度について，のときRiskReductionImportanceは1に近付く：

無関係な成分の重要度は1である：

Wolfram Research (2012), RiskReductionImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/RiskReductionImportance.html.

テキスト

Wolfram Research (2012), RiskReductionImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/RiskReductionImportance.html.

CMS

Wolfram Language. 2012. "RiskReductionImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RiskReductionImportance.html.

APA

Wolfram Language. (2012). RiskReductionImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RiskReductionImportance.html

BibTeX

@misc{reference.wolfram_2024_riskreductionimportance, author="Wolfram Research", title="{RiskReductionImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/RiskReductionImportance.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_riskreductionimportance, organization={Wolfram Research}, title={RiskReductionImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/RiskReductionImportance.html}, note=[Accessed: 22-November-2024 ]}