Roots

Roots[lhs==rhs,var]

yields a disjunction of equations which represent the roots of a polynomial equation.

Details and Options

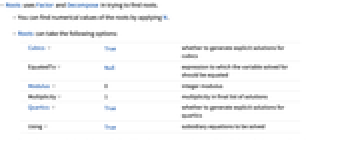
  • Roots uses Factor and Decompose in trying to find roots.
  • You can find numerical values of the roots by applying N.
  • Roots can take the following options:
  • Cubics Truewhether to generate explicit solutions for cubics
    EquatedTo Nullexpression to which the variable solved for should be equated
    Modulus 0integer modulus
    Multiplicity 1multiplicity in final list of solutions
    Quartics Truewhether to generate explicit solutions for quartics
    Using Truesubsidiary equations to be solved
  • Roots is generated when Solve and related functions cannot produce explicit solutions. Options are often given in such cases.
  • Roots gives several identical equations when roots with multiplicity greater than one occur.

Examples

open allclose all

Basic Examples  (1)

Find roots of univariate polynomial equations:

Scope  (7)

Equation with exact numeric coefficients:

Equation with symbolic coefficients:

General equations of degree five and higher cannot be solved in radicals:

This equation of degree nine is solved in radicals using factorization and decomposition:

An equation with inexact numeric coefficients:

Multiple roots are repeated the corresponding number of times:

Find roots over the integers modulo 7:

Options  (10)

Cubics  (3)

By default Roots uses the general formulas for solving cubic equations in radicals:

With Cubics->False, Roots does not use the general formulas for solving cubics in radicals:

Solving this cubic equation in radicals does not require the general formulas:

EquatedTo  (1)

Use EquatedTo to specify the left-hand side of the returned equations:

Modulus  (1)

Find roots over the integers modulo 12:

Multiplicity  (1)

With Multiplicity->n, the multiplicity of each root is multiplied by n:

Quartics  (3)

By default Roots uses the general formulas for solving quartic equations in radicals:

With Quartics->False, Roots does not use the general formulas for solving quartics:

Solving this quartic equation in radicals does not require the general formulas:

Using  (1)

Specify equations satisfied by symbolic parameters:

Properties & Relations  (5)

Solutions returned by Roots satisfy the equation:

Use ToRules to convert equations returned by Roots to replacement rules:

Solve uses Roots to find solutions of univariate equations and returns replacement rules:

Roots finds all complex solutions:

Use Reduce to find solutions over specified domains:

Use FindInstance to find one solution:

Use Solve or Reduce to find solutions of systems of multivariate equations:

Use Reduce to find solutions of systems of equations and inequalities:

Use NRoots to find numeric approximations of roots of a univariate equation:

Wolfram Research (1988), Roots, Wolfram Language function, https://reference.wolfram.com/language/ref/Roots.html.

Text

Wolfram Research (1988), Roots, Wolfram Language function, https://reference.wolfram.com/language/ref/Roots.html.

CMS

Wolfram Language. 1988. "Roots." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Roots.html.

APA

Wolfram Language. (1988). Roots. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Roots.html

BibTeX

@misc{reference.wolfram_2024_roots, author="Wolfram Research", title="{Roots}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Roots.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_roots, organization={Wolfram Research}, title={Roots}, year={1988}, url={https://reference.wolfram.com/language/ref/Roots.html}, note=[Accessed: 22-November-2024 ]}