SignTest
SignTest[data]
data の中央値が0かどうか調べる.
SignTest[{data1,data2}]
data1– data2 の中央値が0かどうか調べる.
SignTest[dspec,μ0]
μ0について位置尺度を調べる.
SignTest[dspec,μ0,"property"]
"property"の値を返す.
詳細とオプション



- SignTestは,帰無仮説
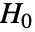 と対立仮説
と対立仮説 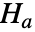 で検定を行う.
で検定を行う. -
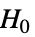
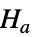
data 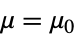
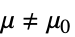
{data1,data2} 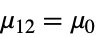
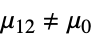
- ただし,μ は data の母集団中央値であり,μ12は2つのデータ集合のペアになった差分
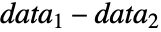 の中央値である.
の中央値である. - デフォルトで,確率値つまり
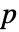 値が返される.
値が返される. - 小さい
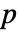 値は
値は 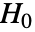 が真である可能性が低いことを示す.
が真である可能性が低いことを示す. - dspec 中のデータは一変量{x1,x2,…}でも多変量{{x1,y1,…},{x2,y2,…},…}でもよい.
- 2つのサンプルを与える場合,両者は同じ長さでなければならない.
- 引数 μ0は実数あるいはデータの次元と同じ長さの実ベクトルでよい.
- SignTest[dspec,μ0,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す.これは htd["property"]として追加的な検定結果と特性の抽出に使うことができる.
- SignTest[dspec,μ0,"property"]を使って直接"property"の値を与えることができる.
- 検定結果のレポートに関連する特性
-
"DegreesOfFreedom" 検定で使用される自由度 "PValue" 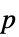 値のリスト
値のリスト "PValueTable" 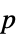 値のフォーマットされた表
値のフォーマットされた表"ShortTestConclusion" 検定結果の簡単な説明 "TestConclusion" 検定結果の説明 "TestData" 検定統計と 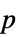 値のペアのリスト
値のペアのリスト"TestDataTable" 検定統計と 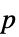 値のフォーマットされた表
値のフォーマットされた表"TestStatistic" 検定統計のリスト "TestStatisticTable" 検定統計のフォーマットされた表 - 一変量のサンプルについては,ペアになったサンプルの中央値についてSignTestは符号検定を行う.検定統計はBinomialDistribution[n,1/2] に従うと仮定される.ただし,n は dspec 中の μ0と等しくない要素数である.
- 多変量のサンプルについては,SignTestは空間的符号を用いてアフィン不変量検定を行う.検定統計はChiSquareDistribution[dim]に従うと仮定される.ただし,dim は dspec の次元である.
- 使用可能なオプション
-
AlternativeHypothesis "Unequal" 対立仮説のための不等式 MaxIterations Automatic 多変量中央値検定のための最大反復回数 Method Automatic 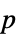 値を計算するメソッド
値を計算するメソッドSignificanceLevel 0.05 診断とレポートのための切捨て - SignTestでは,
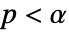 のときにのみ
のときにのみ 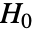 が棄却されるような切捨て
が棄却されるような切捨て 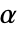 が選択される.特性"TestConclusion"および"ShortTestConclusion"で使われる
が選択される.特性"TestConclusion"および"ShortTestConclusion"で使われる 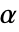 の値はSignificanceLevelオプションで制御される.デフォルトで,
の値はSignificanceLevelオプションで制御される.デフォルトで,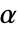 は0.05に設定されている.
は0.05に設定されている.
例題
すべて開くすべて閉じる例 (4)
特性を繰り返し抽出するためにHypothesisTestDataオブジェクトを作成する:
スコープ (13)
検定 (10)
Automaticを使うことは,ゼロの中央値について検定することと同じである:
多変量母集団の中央値ベクトルがゼロベクトルであるかどうかを検定する:
2つの多変量母集団の中央値の差分ベクトルがゼロベクトルであるかどうかの検定を行う:
繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する:
HypothesisTestDataオブジェクトから特性を抽出する:
オプション (9)
AlternativeHypothesis (3)
Method (3)
デフォルトでは,一変量データについては,BinomialDistributionを使って ![]() 値が計算される:
値が計算される:
アプリケーション (2)
8人の患者に対して,新しい睡眠薬について検定が行われた.それぞれの被験者が眠りにつくまでにかかる時間(単位:分)が薬を飲んだ夜とプラシーボを飲んだ夜について記録された:
SignTestは睡眠薬とプラシーボの違いを検出しない:
データ集合は非常に小さいが,正規性についての検定には失敗しない:
より強力なPairedTTestは,睡眠薬によって眠りにつく時間が大幅に削減されたことを示す:
数学と科学の評価が低い10人の学生のグループが個別指導プログラムに参加するように頼まれた.もとの評価に似たテストがプログラム後に行われた.学生たちの両方の評価における数学と科学の点数は以下の通りである:
特性と関係 (6)
概念的には,SignTestはデータ集合内の正の符号の数を数える:
一変量データについては,検定統計はBinomialDistributionに従い,ゼロを無視する:
SignTestは一般に,位置についてのその他の仮説検定に比べて弱い:
多変量データについては,検定統計を計算する場合,空間符号を使う:
空間中央値が非零である場合,空間符号はクラスタ化することが多い:
検定統計はChiSquareDistribution[p]に従う:
符号検定は,入力がTimeSeriesのときにのみ値に使うことができる:
符号検定は,入力がTemporalDataのときはすべての値に同時に使うこができる:
テキスト
Wolfram Research (2010), SignTest, Wolfram言語関数, https://reference.wolfram.com/language/ref/SignTest.html.
CMS
Wolfram Language. 2010. "SignTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SignTest.html.
APA
Wolfram Language. (2010). SignTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SignTest.html