SkellamDistribution
SkellamDistribution[μ1,μ2]
表示形状参数为 μ1 和 μ2 的 Skellam 分布.
更多信息
- Skellam 分布中的整数
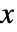 的概率密度与
的概率密度与 ![(mu_1/mu_2)^(x/2) TemplateBox[{x, {2, , {sqrt(, {{mu, _, 1}, , {mu, _, 2}}, )}}}, BesselI] (mu_1/mu_2)^(x/2) TemplateBox[{x, {2, , {sqrt(, {{mu, _, 1}, , {mu, _, 2}}, )}}}, BesselI]](Files/SkellamDistribution.zh/2.png) 成正比.
成正比. - SkellamDistribution[μ1,μ2] 是
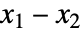 的分布,其中
的分布,其中 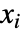 是参数为 μi 的独立泊松分布.
是参数为 μi 的独立泊松分布. - SkellamDistribution 允许 μ1 和 μ2 为任意正实数.
- SkellamDistribution 可以和 Mean、CDF 和 RandomVariate 等函数一起使用.
背景
- SkellamDistribution[μ1,μ2] 表示一个离散统计分布,定义于整数值
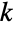 上,由正实数 μ1 和 μ2 确定,并且定义为差 XY1-Y2 的分布,其中 Y1PoissonDistribution[μ1] 和 Y2PoissonDistribution[μ2] 是均值分别为 μ1 和 μ2 的独立变数. Skellam 分布的概率密度函数 (PDF) 是离散和单峰的,其整体形状(高度、展布和最大值的水平位置)由 μ1 和 μ2 的值确定.
上,由正实数 μ1 和 μ2 确定,并且定义为差 XY1-Y2 的分布,其中 Y1PoissonDistribution[μ1] 和 Y2PoissonDistribution[μ2] 是均值分别为 μ1 和 μ2 的独立变数. Skellam 分布的概率密度函数 (PDF) 是离散和单峰的,其整体形状(高度、展布和最大值的水平位置)由 μ1 和 μ2 的值确定. - Skellam 分布由 J. G. Skellam 于二十世纪四十年代中期导出,用来模拟来自不同总体的两个服从泊松分布的变数的理论分布. 从那时起,在图像分析中就用 Skellam 分布来研究有环境噪声时图像的区别,以及研究在两个地点和/或两个时间段事故发生次数的差别. Skellam 分布还被用来模拟体育比赛分数、股票价格、排队模型和基因表达等现象.
- RandomVariate 可用来给出一个或更多机器精度或任意精度(后者可通过设置 WorkingPrecision 选项获得)的 Skellam 分布中的伪随机变数. Distributed[x,SkellamDistribution[μ1,μ2]],更简洁的式子为 xSkellamDistribution[μ1,μ2],可用来断定随机变量 x 服从 Skellam 分布. 它也可以被用在诸如 Probability、NProbability、Expectation 和 NExpectation 这样的函数中.
- 通过使用 PDF[SkellamDistribution[μ1,μ2],x] 和 CDF[SkellamDistribution[μ1,μ2],x],可以得到 Skellam 分布的概率密度和累积分布函数,但我们要注意,Skellam 分布的概率分布函数的解析式是不存在的. 可以用 Mean、Median、Variance、Moment 和 CentralMoment 来分别计算均值、中位数、方差、原始矩和中心矩,同时,可以使用 DiscretePlot 来绘制上述各量的图形.
- 可以用 DistributionFitTest 来检测一个数据集是否符合 Skellam 分布,根据给定数据,用 EstimatedDistribution 来估计 Skellam 参数分布,而 FindDistributionParameters 则可用来将数据拟合成 Skellam 分布. 用 ProbabilityPlot 指令可以产生给定数据的 CDF 与符号式 Skellam 分布的 CDF 的比较图,QuantilePlot 则能绘制给定数据的分位数和符号式 Skellam 分布的分位数的比较图.
- 可以用 TransformedDistribution 来表示转换过的 Skellam 分布,用 CensoredDistribution 表示截尾后位于上限和下限值之间的数据的分布,而 TruncatedDistribution 则表示删失后位于上限和下限值之间的数据的分布. CopulaDistribution 可用来构建包含 Skellam 分布的高维分布, ProductDistribution 可计算独立分量包括 Skellam 分布的联合分布.
- SkellamDistribution 和许多其他统计分布有关. 它是 PoissonDistribution 的转换 (TransformedDistribution),是由于 SkellamDistribution[μ1,μ2] 等价于 x-y 的分布,其中 xPoissonDistribution[μ1] 和 yPoissonDistribution[μ2]. SkellamDistribution 还与 PoissonConsulDistribution、CompoundPoissonDistribution 和 PolyaAeppliDistribution 密切相关.
范例
打开所有单元关闭所有单元范围 (7)
应用 (3)
SkellamDistribution 的累积分布函数是右连续函数的一个例子:
芝加哥小熊队和圣路易斯红雀队在2004年和2008年间获得平均每场比赛 4.72 和 4.88 的分数. 假设每个队是独立参赛的且按 PoissonDistribution 进行分布,分别具有均值:
到达装载码头的包的数量服从 PoissonDistribution,平均每小时30个. 从码头搬走包服从 PoissonDistribution,为平均每小时25个. 求剩余在码头的包的数量的分布:
Wolfram Research (2010),SkellamDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SkellamDistribution.html.
文本
Wolfram Research (2010),SkellamDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SkellamDistribution.html.
CMS
Wolfram 语言. 2010. "SkellamDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SkellamDistribution.html.
APA
Wolfram 语言. (2010). SkellamDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SkellamDistribution.html 年