SmithDelayCompensator

SmithDelayCompensator[sys,con]

gives the Smith compensator for the time-delay system sys and the delay-free controller con.

Details and Options

  • The system can be a StateSpaceModel or TransferFunctionModel object.
  • A Smith delay compensator is a controller for time-delay systems that eliminates internal delays in the closed-loop system.
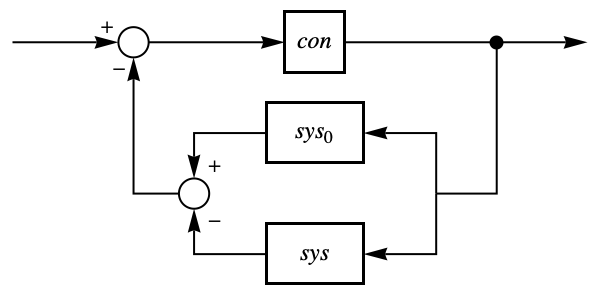
  • Block diagram of a Smith predictor with controller con and system model sys, where sys0 denotes all delays being set to zero:

Examples

open allclose all

Basic Examples  (1)

A compensator for a time-delay TransferFunctionModel with feedback gain k:

Scope  (2)

A symbolic controller for a time-delay TransferFunctionModel with a PI controller:

A compensator for a StateSpaceModel with internal delays:

Applications  (2)

Use a Smith predictor to design a pole-placement controller for a time-delay system:

The closed-loop system has no internal delays:

A chemical reactor train (Ogunnaike and Ray, 1979):

A Smith predictor for a diagonal feedback matrix:

Compare the closed-loop response with and without the Smith predictor:

Properties & Relations  (1)

A Smith predictor for a time-delay TransferFunctionModel and PID controller:

The resulting closed-loop system has no internal delays:

Wolfram Research (2012), SmithDelayCompensator, Wolfram Language function, https://reference.wolfram.com/language/ref/SmithDelayCompensator.html.

Text

Wolfram Research (2012), SmithDelayCompensator, Wolfram Language function, https://reference.wolfram.com/language/ref/SmithDelayCompensator.html.

CMS

Wolfram Language. 2012. "SmithDelayCompensator." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SmithDelayCompensator.html.

APA

Wolfram Language. (2012). SmithDelayCompensator. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SmithDelayCompensator.html

BibTeX

@misc{reference.wolfram_2025_smithdelaycompensator, author="Wolfram Research", title="{SmithDelayCompensator}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/SmithDelayCompensator.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_smithdelaycompensator, organization={Wolfram Research}, title={SmithDelayCompensator}, year={2012}, url={https://reference.wolfram.com/language/ref/SmithDelayCompensator.html}, note=[Accessed: 18-April-2025 ]}