SpatialMedian

SpatialMedian[{x1,x2,…}]

要素 の空間中央値を与える．

SpatialMedian[data]

data の異なるいくつかの形式についての空間中央値を与える．

詳細とオプション

  • SpatialMedianは，幾何学的中央値，中間地点，1-中央値としても知られている．
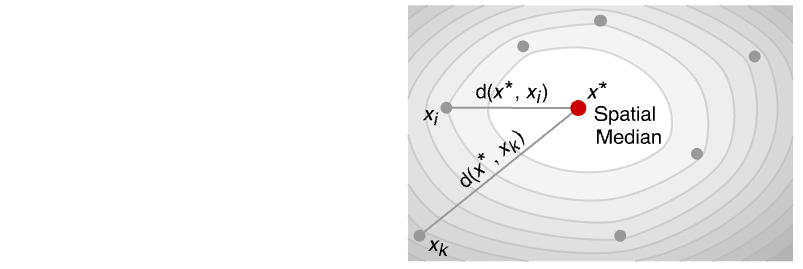
  • SpatialMedianは，ロバストな位置測度であり，データ内の各点までの距離が最小な点を与える．
  • SpatialMedianは，重みがない場合は x^*=ArgMin[sum_(i=1)^nd(x,x_i),x]に，重みがある場合は x^*=ArgMin[sum_(i=1)^nw_i d(x,x_i),x]に等しい．
  • データ data には次の形と解釈がある．
  • {x1,x2,…}一変量数値データ
    {{x1,y1,…},{x2,y2,…},…}多変量数値データ
    {GeoPosition[…],GeoPosition[…],…}測地位置のリスト
    GeoPosition[…]測地位置の配列
    WeightedData[…]重み付きのデータ
  • ユークリッド距離のもとでは，SpatialMedianは一次元の場合の中央値と一致する．多次元の場合は，点が同一線上にない場合は常に空間中央値は一意的である．
  • 次のオプションを与えることができる．
  • AccuracyGoalAutomatic目標確度
    DistanceFunction Automatic使用する距離測度
    MaxIterationsAutomatic使用する反復の最大数
    Method Automatic使用するメソッド
    PrecisionGoalAutomatic目標精度
    WorkingPrecisionAutomatic内部計算に使われる精度
  • デフォルトで，異なるタイプの要素について次の距離関数が使われる．
  • EuclideanDistance数値データ
    GeoDistance地理空間データ
  • Method{"InitialPoint"{x0,y0,…}}と設定すると．SpatialMedianの計算にカスタムの初期点を使うことができる．

例題

すべて開くすべて閉じる

例  (3)

ベクトルリストの空間中央値を求める：

与えられた重みを使ってベクトルリストの空間中央値を求める：

地理位置の空間中央値を計算する：

スコープ  (5)

精度が異なる同じ入力：

空間中央値はWeightedDataに使うことができる：

大きい配列の空間中央値：

重み付きの空間中央値：

単位付き数量を含むデータの空間中央値：

測地位置の空間中央値を計算する：

オプション  (4)

DistanceFunction  (2)

デフォルトで，EuclideanDistanceは数値データに使われる：

ChessboardDistanceは，距離が最も大きい次元しか考慮しない：

DistanceFunctionはシンボルとして与えることができる：

純関数として与えることもできる：

Method  (2)

空間中央値の反復手続における初期点を指定する：

"NMinimize"とFindMinimumのメソッドオプションを使うことができる：

指定のDistanceFunctionと一緒に使う：

アプリケーション  (8)

外れ値がある場合の多変量位置のロバスト推定を得る：

極値はMeanに大きく影響する：

ガウス混合分布からのデータについて考える：

Meanで中心を推定する：

サンプル平均推定器は非ガウスデータについては大きく広がる．推定器の標準偏差は次のようになる：

SpatialMedianで中心を推定する：

ブート処理で広がりを見積もる．空間中央値は平均よりも広がりが小さい：

GOOG，MSFT，FB，AAPL，INTCの5社の2015年における株価を五次元データとして考察する：

MeanとSpatialMedianを使って対数利益率を計算し，中心を推定する：

MultivariateTDistributionでデータをフィットし，位置母数を抽出する：

与えられた株価について，空間中央値推定器は経験的平均値よりも，多変量 t 分布の位置母数に近い推定を与える：

点の数が3のとき，空間中央値はフェルマ点でもある：

各辺について正三角形を作る：

フェルマ点を幾何学的に作り，SpatialMedianの結果（赤）と比較する：

凸多角形からのサンプル点：

ランダムな点の空間中央値を計算することで，多角形の中心を推定する：

都市の位置に基づいてカリフォルニアの空間中央値を求める：

人口で重みを付けた都市の位置に基づいてカリフォルニアの空間中央値を求める：

都市の位置（灰色），重みなしの空間中央値（赤），重みありの空間中央値（黒）を描画する：

地球表面上で十分離れている地理位置については，空間中央値は選択された距離関数に大きく依存する：

GeoPositionによる空間中央値：

EuclideanDistanceによる投影座標点の空間中央値：

空間中央値と都市の位置を示す：

地理実体の重心は一様にサンプルされた地理位置の空間中央値を使って近似することができる．スペインの国多角形を得る：

領域からサンプル点を取り，対応する空間中央値を計算する：

空間中央値に最も近い都市を求める：

結果を可視化する：

特性と関係  (5)

SpatialMedianは多変量位置測度である：

空間中央値を計算する：

Meanもまた位置測度である：

データ点を空間中央値および平均とともに可視化する：

SpatialMedianは空間点の L1位置推定器である：

FindMinimumによる定義からSpatialMedianを計算する：

距離関数の和を可視化する：

Mean（あるいは空間平均）は空間点の L2位置推定器である：

FindMinimumによる定義からMeanを計算する：

距離関数の和を可視化する：

SpatialMedianは，一変量データについてはMedianに等しい：

多変量データについてのManhattanDistanceにおけるSpatialMedianはMedianに等しい：

SpatialMedianは，距離の和を最小にする領域内の点を求める：

CentralFeatureは，距離の和を最小にするデータに属する点を求める：

CentralFeatureについての距離の和はSpatialMedianについてのそれ以上である：

Wolfram Research (2017), SpatialMedian, Wolfram言語関数， https://reference.wolfram.com/language/ref/SpatialMedian.html.

テキスト

Wolfram Research (2017), SpatialMedian, Wolfram言語関数， https://reference.wolfram.com/language/ref/SpatialMedian.html.

CMS

Wolfram Language. 2017. "SpatialMedian." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpatialMedian.html.

APA

Wolfram Language. (2017). SpatialMedian. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpatialMedian.html

BibTeX

@misc{reference.wolfram_2024_spatialmedian, author="Wolfram Research", title="{SpatialMedian}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/SpatialMedian.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_spatialmedian, organization={Wolfram Research}, title={SpatialMedian}, year={2017}, url={https://reference.wolfram.com/language/ref/SpatialMedian.html}, note=[Accessed: 22-November-2024 ]}