SpatialRandomnessTest

SpatialRandomnessTest[pdata]

点集合 pdata が観測領域上に均一に分布しているかどうかの検定を行う．

SpatialRandomnessTest[pdata,"property"]

"property"の値を返す．

詳細とオプション

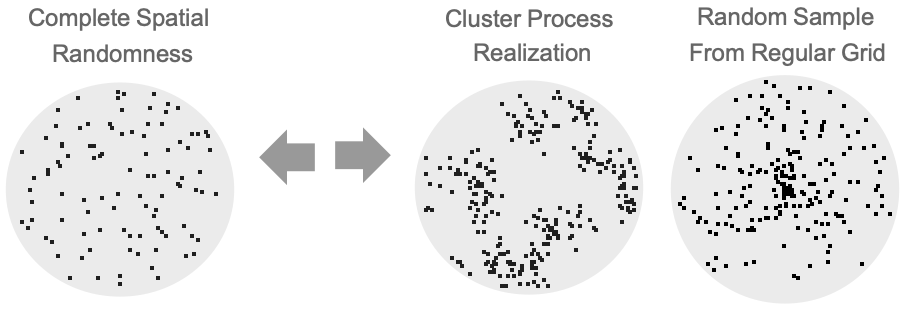
  • SpatialRandomnessTestは，pdata がPoissonPointProcessからのものであるという帰無仮説 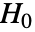とそうではないという対立仮説 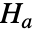で適合度仮説検定を行う．
  • デフォルトで，確率値，つまり 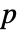値が返される．
  • 小さい 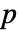値は pdata がPoissonPointProcessからのものである可能性が低いことを示唆している．
  • 点データ pdata は次の形式でよい．
  • {p1,p2,…}点 pi
    GeoPosition[…],GeoPositionXYZ[…],…地理的な点
    SpatialPointData[…]空間点の集合
    {pts,reg}点集合 pts と観測領域 reg
  • 観測領域 reg は，与えられていなければRipleyRassonRegionを使って自動的に計算される．
  • SpatialRandomnessTest[pdata,"test"]は"test"に従って 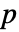値を報告する．
  • SpatialRandomnessTest[pdata,All]はすべての検定を選択する．
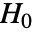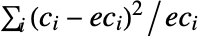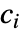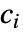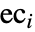  • 帰無仮説 の下では，pdata 中の点はPoissonPointProcess[λ]から取られる．これは，点が観測領域 reg 上で一様に分布していなければならないことを意味する．点をビン分割することで，標準ビン数の残差は近似カイ分布に従っていなければならず，数 は多項分布に従っていなければならない．ただし，と はそれぞれビン i 中の数と期待数である．
  • 次は，指定可能な検定である．
  • "BesagL"半径の関数として直線であると予想され，統計的検出力が遅くかつ高いBesagLに基づく
    "ChiSquare"標準ビン数の残余が，カイ2乗分布に従って高速で近似的であると予想されるビン分割に基づく
    "ModifiedChiSquare"数が多項分布に従っていると予想される，小さいサンプル数については厳密で大きいデータには"ChiSquare"を使うビン分割に基づく
  • SpatialRandomnessTest[pdata,"HypothesisTestData"]は，htd["property"]を使った追加的な検定結果と特性の抽出に使えるHypothesisTestDataオブジェクト htd を返す．
  • SpatialRandomnessTest[pdata,"property"]を使って"property"の値を直接与えることができる．
  • 次は，検定結果の報告に関連する特性である．
  • "AllTests"適用可能な全検定のリスト
    "AutomaticTest"Automaticが使われた場合に選択される検定
    "PValue" 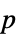値のリスト
    "PValueTable" 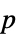値のフォーマットされた表
    "ShortTestConclusion"検定結果の短い説明
    "TestConclusion"検定結果の説明
    "TestData"検定統計と 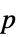値のペアのリスト
    "TestDataTable" 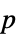値と検定統計のフォーマットされた表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマットされた表
  • 次は，使用可能なオプションである．
  • SignificanceLevel 0.05診断と報告のためのカットオフ

例題

すべて開くすべて閉じる

例  (2)

円板上の一様点分布：

このデータは均一強度の点過程から来ている：

地理領域上に分布する点：

データは均一強度の点過程からのものである：

スコープ  (10)

検定  (7)

空間ランダム性の検定を行う：

点が均一に分布しているときは， 値は一般に大きい：

空間的に不均一なときは， 値は一般に小さい：

空間ランダム性について特定の検定を行う：

特定の検定の特性を抽出する：

Automaticを使って"AutomaticTest"オプションを適用する：

特性"AutomaticTest"を使ってどの検定が選ばれたかが判定できる：

データに適したすべての検定を同時に実行する：

特性"AllTests"を使ってどの検定が使われたかを識別する：

特性を繰り返し抽出するためにHypothesisTestDataオブジェクトを作る：

抽出に使用可能な特性：

HypothesisTestDataオブジェクトからいくつかの特性を抽出する：

"ChiSquare"検定からの 値と検定統計：

任意数の特性を同時に抽出する：

"ChiSquare"検定からの 値と検定統計：

報告  (3)

選択した検定からの結果を表にする：

適切なすべての検定結果の完全な表：

選択した検定結果の表：

レポートをカスタマイズするために検定表から項目を取り出す：

値は0.05より上なので，このレベルで を棄却するに足る証拠はない：

有意水準は，"TestConclusion"と"ShortTestConclusion"に使われる：

オプション  (1)

SignificanceLevel  (1)

有意水準を指定する：

検定の結論は異なるかもしれない：

完全な検定の結論：

おもしろい例題  (1)

帰無仮説の下での"ModifiedChiSquare"検定統計の分布：

Wolfram Research (2020), SpatialRandomnessTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/SpatialRandomnessTest.html.

テキスト

Wolfram Research (2020), SpatialRandomnessTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/SpatialRandomnessTest.html.

CMS

Wolfram Language. 2020. "SpatialRandomnessTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpatialRandomnessTest.html.

APA

Wolfram Language. (2020). SpatialRandomnessTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpatialRandomnessTest.html

BibTeX

@misc{reference.wolfram_2024_spatialrandomnesstest, author="Wolfram Research", title="{SpatialRandomnessTest}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/SpatialRandomnessTest.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_spatialrandomnesstest, organization={Wolfram Research}, title={SpatialRandomnessTest}, year={2020}, url={https://reference.wolfram.com/language/ref/SpatialRandomnessTest.html}, note=[Accessed: 18-November-2024 ]}