BinomialPointProcess
BinomialPointProcess[n,reg]
represents a binomial point process with n points in the region reg.
Details
- BinomialPointProcess[n,reg] generates points that are uniformly distributed in reg with the total number of points equal to n.
- Typical uses include cases where the total number of points is specified, such as a known number of wireless transceivers in a region, number of fish in an aquarium, etc.
- BinomialPointProcess and PoissonPointProcess both yield a uniform distribution of points over a region. The former uses a deterministic number of points and the latter a random number of points.
- The number of points inside a bounded subregion
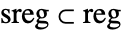follows BinomialDistribution[n,p] with p=RegionMeasure[sreg]/RegionMeasure[reg]. - The number of points in disjoint subregions of reg for a binomial point process is not independent.
- For disjoint subregions
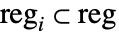that satisfy 
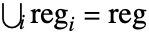, the joint distribution of the number of points inside the subregions 
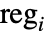with volume 
follows MultinomialDistribution[n,{ν1/ν,…,νn/ν}], where 
is the volume of reg. - BinomialPointProcess[n,reg] is PoissonPointProcess[μ] conditioned on the event
with 
a random variable following PointCountDistribution[PoissonPointProcess[μ],reg]. - BinomialPointProcess allows n to be any positive integer and reg any parameter-free region.
- BinomialPointProcess can be used with such functions as RipleyK and RandomPointConfiguration.
Examples
open allclose allBasic Examples (2)
Scope (2)
Sample from any valid RegionQ whose RegionEmbeddingDimension is equal to its RegionDimension:
Applications (1)
Properties & Relations (4)
The number of points in a BinomialPointProcess is defined by n:
Simulate BinomialPointProcess over a unit disk:
The corresponding PointCountDistribution over a bounded subset:
Compare the histogram of point counts in the subset with the PDF:
Fit a BinomialDistribution to the point counts:
Test against theoretical distribution:
PointCountDistribution over region covering:
Point count distribution for the covering:
Compute void probabilities for a binomial point process:
Binomial point process is stationary—the intensity is translation invariant:
Text
Wolfram Research (2020), BinomialPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/BinomialPointProcess.html.
CMS
Wolfram Language. 2020. "BinomialPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BinomialPointProcess.html.
APA
Wolfram Language. (2020). BinomialPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BinomialPointProcess.html