SpearmanRankTest

SpearmanRankTest[v1,v2]

ベクトル v1と v2が独立かどうかの検定を行う．

SpearmanRankTest[m1,m2]

行列 m1と m2が独立かどうかの検定を行う．

SpearmanRankTest[…,"property"]

"property"の値を返す．

詳細とオプション

  • SpearmanRankTestは，v1と v2に対して，ベクトルが独立であるという帰無仮説 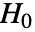と，そうではないという対立仮説 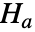で仮説検定を行う．
  • デフォルトで，確率値つまり 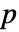値が返される．
  • 小さい 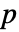値は 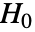が真である可能性が低いことを示す．
  • 引数 v1と v2 は任意の同じ長さの実ベクトルあるいは実行列でよい．
  • SpearmanRankTestはSpearmanRho[v1,v2]で計算されたSpearmanの順位相関 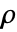に基づいている．
  • 行列の検定の際は，検定統計は内部の標準的な空間順位に基づいておりChiSquareDistribution[r*s]に漸近的に従う．ただし，r と s はそれぞれ m1と m2の大きさである．検定はアフィン変換の下で不変である．
  • SpearmanRankTest[v1,v2,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．このオブジェクトは，htd["property"] の形を使った追加的な検定結果と特性の抽出に使える．
  • SpearmanRankTest[v1,v2,"property"]を使って"property"の値を直接与えることができる．
  • 検定結果のレポートに関連する特性
  • "DegreesOfFreedom"検定の自由度
    "PValue"検定の 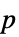値
    "PValueTable" 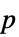値を含むフォーマットされた表
    "ShortTestConclusion"検定結果の短い記述
    "TestConclusion"検定結果の記述
    "TestData"検定統計量と 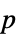値を含むリスト
    "TestDataTable" 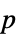値と検定統計量のフォーマットされた表
    "TestStatistic"検定統計量
    "TestStatisticTable"検定統計量を含むフォーマットされた表
  • 使用可能なオプション
  • AlternativeHypothesis "Unequal"対立仮説のための不等式
    MaxIterations Automatic多変量検定の際の最大反復回数
    Method Automatic 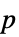値の計算に使用するメソッド
    SignificanceLevel 0.05診断とレポートのための切捨て
  • 独立性の検定については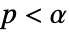， のときにのみ 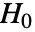が拒絶されるような切捨て 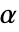が選ばれる．"TestConclusion"特性と"ShortTestConclusion"特性に使われる 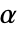の値はSignificanceLevelオプションで制御される．デフォルトで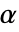， は0.05に設定されている．

例題

すべて開くすべて閉じる

例  (2)

2つのベクトルが独立かどうかの検定を行う：

2つの行列が独立かどうかの検定を行う：

0.05の水準では独立性を棄却するための十分な証拠はない：

スコープ  (8)

検定  (5)

2つのベクトルが独立かどうかの検定を行う：

ベクトルが独立のとき， 値は一般に大きくなる：

従属関係がある場合は 値は一般に小さくなる：

2つの行列が独立かどうかの検定を行う：

従属行列の場合には 値は一般に小さくなる：

行列が独立のとき， 値は一般に大きくなる：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出可能な特性：

HypothesisTestDataオブジェクトからいくつかの特性を抽出する：

検定からの 値と検定統計量：

任意数の特性を同時に抽出する：

検定からの 値と検定統計量：

レポート  (3)

検定結果を表にする：

検定結果の表：

レポートをカスタマイズするために検定表から項目を取り出す：

値あるいは検定統計量を表にする：

表からの 値：

表からの検定統計量：

オプション  (9)

AlternativeHypothesis  (3)

デフォルトで両側検定が行われる：

両側検定あるいは代りの片側検定を行う：

両側検定：

2つの片側検定：

多変量検定はもとから両側検定である：

これは帰無分布の形による：

MaxIterations  (1)

多変量検定に使う反復の最大回数を設定する：

デフォルトで，が使われる：

設定値を低くすると計算時間は短くなるかもしれないが，収束しなくなる可能性がある：

Method  (4)

デフォルトで， 値は漸近的検定統計量分布を使って計算される：

値は置換法を使って得ることができる：

使用する置換回数を設定する：

デフォルトで，回のランダムな置換が使われる：

ランダムな置換の生成に使うシードを設定する：

SignificanceLevel  (1)

有意水準は"TestConclusion"と"ShortTestConclusion"に使われる：

特性と関係  (9)

ベクトル間の比較の際は，検定統計がSpearmanRhoとして計算される：

検定統計は の下でStudentTDistribution[n-2]に従う：

より大きい場合，検定統計はChiSquareDistribution[r*s]に従う：

行列の比較の場合は，検定統計はアフィン変換の下で不変である：

CorrelationTestを使ってSpearmanの 値の特別な値の検定を行う：

に対して検定を行う：

IndependenceTestを使って適切な独立性の検定を選ぶことができる：

SpearmanRankTestは使用可能な検定の一つである：

SpearmanRankTestは単調依存しか検出しない：

HoeffdingDTestを使うと，より広い範囲の依存構造が検出ができる：

Spearmanの順位検定は，入力がTimeSeriesのときにのみ値に使うことができる：

Spearmanの順位検定は，入力がTemporalDataのときは値全体に同時に使うことができる：

時間データの選択された成分について明示的に検定を行う：

値を直接使う：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

Wolfram Research (2012), SpearmanRankTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/SpearmanRankTest.html.

テキスト

Wolfram Research (2012), SpearmanRankTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/SpearmanRankTest.html.

CMS

Wolfram Language. 2012. "SpearmanRankTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpearmanRankTest.html.

APA

Wolfram Language. (2012). SpearmanRankTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpearmanRankTest.html

BibTeX

@misc{reference.wolfram_2024_spearmanranktest, author="Wolfram Research", title="{SpearmanRankTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/SpearmanRankTest.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_spearmanranktest, organization={Wolfram Research}, title={SpearmanRankTest}, year={2012}, url={https://reference.wolfram.com/language/ref/SpearmanRankTest.html}, note=[Accessed: 22-November-2024 ]}