WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

SpearmanRho

SpearmanRho[v₁,v₂]

ベクトル v₁と v₂についてのSpearmanの順位相関係数を与える．

行列 m についてのSpearmanの順位相関係数を与える．

SpearmanRho[m₁,m₂]

行列 m₁と m₂についてのSpearmanの順位相関係数を与える．

SpearmanRho[dist]

多変量記号分布 dist についてのSpearmanの順位相関行列を与える．

SpearmanRho[dist,i,j]

多変量記号分布 dist についての番目のSpearmanの順位相関を与える．

詳細

SpearmanRho[v₁,v₂]は v₁と v₂の間のSpearmanの順位相関係数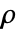を与える．
Spearmanの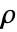は2つのリスト間の順位の差に基づく関連性の尺度で，単調関数が両者の関係をどの程度説明できるかを示す．
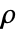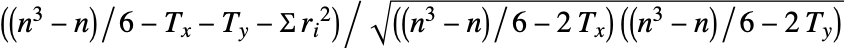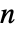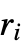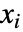Spearmanのはで与えられる．ただし，はLength[xlist]と等しく，はと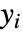の間の順位の差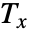，は v₁のタイについての修正項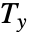，は v₂のタイについての修正項である．
SpearmanRho[{v₁₁,v₁₂,…},{v₂₁,v₂₂,…}]はCorrelation[{r₁₁,r₁₂,…},{r₂₁,r₂₂,…}]に等しい．ただし，r_ijは v_ijに相当するタイ修正された順位である．
引数 v₁と v₂は長さが等しい任意の実ベクトルでよい．
列数が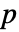の行列 m について，SpearmanRho[m]は m の列間の順位相関の 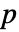× 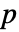行列である．
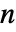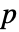× 行列 m₁と 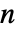× 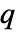行列 m₂については，SpearmanRho[m₁,m₂]は m₁の列と m₂の列の間の順位相関の 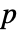× 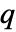行列である．
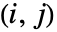
SpearmanRho[dist,i,j]は12 Expectation[F[x]G[y],{x,y}dist_i,j]-3である．ただし，F[x]とG[y]は，それぞれ dist の i 番目と j 番目の周辺分布の累積分布関数であり，dist_i,jは dist の番目の周辺分布である．
SpearmanRho[dist]は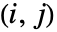番目の項目がSpearmanRho[dist,i,j]で与えられる行列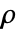を与える．

例題

すべて開くすべて閉じる

例 (4)

2つのベクトルについてのSpearmanの：

行列についてのSpearmanの：

2つの行列についてのSpearmanの：

二変量分布についてのSpearmanのを計算する：

シミュレーションによる値と比較する：

スコープ (7)

データ (4)

厳密な入力は厳密な出力を与える：

近似入力は近似出力を与える：

大規模配列に使うことができる：

SparseArrayデータを使うことができる：

分布と過程 (3)

多変量連続分布についてのSpearmanの：

派生分布についてのSpearmanの：

データ分布について：

時点 s と t におけるランダム過程についてのSpearmanの：

アプリケーション (4)

Spearmanのは，一般に，2つのベクトル間の線形従属性の検出に使われる：

強力な線形従属性がある場合は，の絶対的な大きさは1に近くなる：

線形独立ベクトル間では，この値は0に近くなる：

Spearmanのを使って線形関係を測ることができる：

Spearmanのは単調関係しか検出できない：

HoeffdingDを使ってさまざまな依存構造を検出することができる：

1993年の新車を代表するサンプルについて，さまざまな測定が行われた．変数の中には順序尺度で測られたものがあるので，単調関係を測るのにはSpearmanのがCorrelationよりも適している：

さまざまな基準による散布図の行列：

散布図行列に対応するSpearmanの：

SpearmanRankTestは馬力が大きい車ほど高いことを示している：

1993年には燃費の高さは車の安さを意味していた：

特性と関係 (10)

Spearmanのの範囲は，高い否定的関係を示す-1から高い関係性を示す1までである：

Spearmanのは順位に適用されたCorrelationである：

タイ（同じ値の項）がない場合，順位は順番を使って計算できる：

Spearmanの行列は対称行列である：

Spearmanの行列の対角要素はである：

SpearmanのはKendallTauに関連している：

弱線形関係があるとき，KendallTauはのほぼになる：

変数が完全に単調関係のとき，Spearmanのはまたはに達する：

これは線形関係のみを測るCorrelationとは対照的である：

SpearmanのはCorrelationに比べて外れ値に対する感度が低い：

外れ値がある場合：

外れ値がない場合：

SpearmanRankTestを使って独立性の検定を行う：

あるいは，IndependenceTestを使って適切な検定を自動的に選ぶこともできる：

CorrelationTestを使ってSpearmanのの特定の値についての検定を行う：

値に対しての検定を行う：

二変量連続分布についてのSpearmanの：

トップへ