Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

SpearmanRho

SpearmanRho[v₁,v₂]

给出向量 v₁ 和 v₂ 的 Spearman（斯皮尔曼）等级相关系数 .

给出矩阵 m 的斯皮尔曼等级相关系数 .

SpearmanRho[m₁,m₂]

给出矩阵 m₁ 和 m₂的斯皮尔曼等级相关系数 .

SpearmanRho[dist]

给出多变量符号分布 dist 的斯皮尔曼等级相关矩阵.

SpearmanRho[dist,i,j]

给出多变量符号分布 dist 的第个斯皮尔曼等级相关.

更多信息

SpearmanRho[v₁,v₂] 给出 v₁ 和 v₂ 之间的斯皮尔曼等级相关系数 .
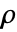斯皮尔曼的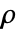是基于两个列表间的等级差异的相关量度，表明单调函数是如何描述它们之间的关系的.
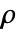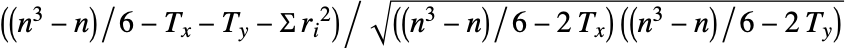斯皮尔曼的由给出，其中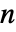等于 Length[xlist]，r_i 是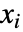和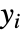间的等级差异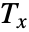，是 v₁ 中关系的校正项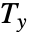，是 v₂ 中关系的校正项.
SpearmanRho[{v₁₁,v₁₂,…},{v₂₁,v₂₂,…}] 等价于 Correlation[{r₁₁,r₁₂,…},{r₂₁,r₂₂,…}]，其中 r_ij 是对应于 v_ij 的关系校正等级.
参变量 v₁ 和 v₂ 可以是任何等长的实数向量.
对于具有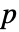列的矩阵 m，SpearmanRho[m] 是一个 m 列间等级相关的 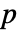× 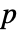矩阵.
对于 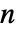× 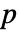矩阵 m₁ 和 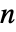× 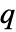矩阵 m₂，SpearmanRho[m₁,m₂] 是一个介于 m₁ 列和 m₂ 列间的等级相关的 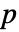× 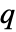矩阵.
SpearmanRho[dist,i,j] 是 12 Expectation[F[x]G[y],{x,y}dist_i,j]-3，其中 F[x] 和 G[y] 是 dist 的第 i 和第 j 边缘的 CDF，dist_i,j 是 dist 的第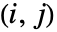边缘.
SpearmanRho[dist] 给出矩阵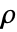，其中第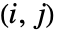项由 SpearmanRho[dist,i,j] 给出.

范例

打开所有单元关闭所有单元

基本范例 (4)

两个向量的斯皮尔曼的：

矩阵的斯皮尔曼的：

两矩阵的斯皮尔曼的：

计算双变量分布的斯皮尔曼的：

比较仿真值：

范围 (7)

数据 (4)

精确输入产生精确输出：

近似输入产生近似输出：

适用于大型矩阵：

可以使用 SparseArray 数据：

分布和过程 (3)

连续多变量分布的斯皮尔曼：

导出分布的斯皮尔曼：

数据分布：

在时间 s 和 t 时随机过程的斯皮尔曼：

应用 (4)

斯皮尔曼一般用于检测两个向量间的线性相关：

的绝对幅度趋于1，给出强线性相关：

对于线性独立向量，该值趋于0：

斯皮尔曼可用于度量线性相关：

斯皮尔曼只能检测单调关系：

HoeffdingD 可用于检测各种相关结构：

度量收集自1993年的新车代表样本. 因为一些变量是按序尺度测量的，Spearman 的比 Correlation 更适合于测量单调相关性：

各种矩阵的散点图矩阵：

斯皮尔曼的对应于散点图的矩阵：

SpearmanRankTest 表明更高马力的车辆更贵：

在1993年较高的燃油经济性意味着更低的价格：

属性和关系 (10)

对于高负和高正关联，斯皮尔曼的的范围从 -1 到 1：

斯皮尔曼的是 Correlation 应用到等级：

没有关系时，等级可用 Ordering 计算：

斯皮尔曼的矩阵是对称的：

斯皮尔曼的矩阵的对角元素为：

斯皮尔曼的与 KendallTau 相关：

假设弱线性关联，KendallTau 趋于的：

如果变量是完全单调相关，斯皮尔曼的将达到或：

相比之下，Correlation 直接测量线性关联：

斯皮尔曼的对异常值，没有 Correlation 敏感：

有异常值：

没有异常值：

使用 SpearmanRankTest 测试独立性：

或者，使用 IndependenceTest 自动选择合适的测试：

使用 CorrelationTest 测试斯皮尔曼的的特殊值：

反测的值：

对于连续双变量分布的斯皮尔曼的：

顶部