Sqrt

Sqrt[z]

または，z の平方根を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
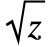  • は，や∖(∖@z∖)と入力できる．
  • Sqrt[z]は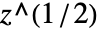，に変換される．
  • Sqrt[z^2]は，自動的には z に変換されない．
  • Sqrt[a b]は，自動的にはSqrt[a]Sqrt[b]に変換されない．
  • これらの変換はPowerExpandを使って行うことができるが，通常，正の実数である引数に対してのみ正確である．
  • 特別な引数の場合，Sqrtは自動的に厳密値を計算する．
  • Sqrtは任意の数値精度で評価できる．
  • Sqrtは自動的にリストに縫い込まれる． »
  • StandardFormではSqrt[z]は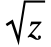と出力される．
  • √z は入力に使うこともできる．√ 文字はsqrtあるいは\[Sqrt]として入力される．

例題

すべて開くすべて閉じる

例  (6)

数値的に評価する：

を使ってを入力する：

負の数の場合は虚数の平方根となる：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

は必ずしも と等しくはない：

と仮定すると に簡約することができる：

スコープ  (39)

数値評価  (7)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率的に評価する：

Sqrtは実数値区間を扱うことができる：

自動縫込みを使って配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のSqrt関数を計算することもできる：

Aroundを使って平均的な場合の統計区間を計算する：

特定の値  (4)

固定点におけるSqrtの値：

ゼロにおける値：

無限大における値：

Solveを使ってとなるような の値を求める：

結果を代入する：

結果を可視化する：

可視化  (4)

Sqrt関数の実部と虚部をプロットする：

と (Surd[x,2])の実部と虚部を比較する：

の実部をプロットする：

の虚部をプロットする：

についての極プロット：

関数の特性  (10)

Sqrtの実領域：

上記はすべての複素数値について定義される：

Sqrtは非負の全実数値に達する：

複素数値の範囲は負の虚軸を除く右半平面である：

分枝切断線における極限を求める：

sqrt または\[Sqrt]で √ 記号を入力し，続けて数字を入力する：

は解析関数ではない：

有理型でもない：

は非減少でも非増加でもない：

しかし，実数値のところでは増加する：

は単射である：

全射ではない：

は定義域では非負である：

は について分枝切断特異点を持つ：

しかし，原点では連続的である：

は凸でも凹でもない：

しかし，実数値のところでは凹である：

微分  (3)

z についての一次導関数：

z についての高次導関数：

z についての高次導関数をプロットする：

z についての 次導関数の式：

積分  (3)

Integrateを使って不定積分を計算する：

不定積分を確かめる：

定積分：

その他の積分例：

級数展開  (4)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似をプロットする：

SeriesCoefficientを使った級数展開における一般項：

一次フーリエ(Fourier)級数：

生成点におけるテイラー展開：

関数の恒等式と簡約  (4)

主定義：

ExpとLogの関係：

は自動的に で置換されるわけではない：

と仮定すると に簡約することができる：

x in TemplateBox[{}, Reals]と仮定するとTemplateBox[{x}, Abs]に簡約することができる：

PowerExpandを使って仮定せずに強制的に簡約することができる：

実変数の x と y を仮定して展開する：

アプリケーション  (4)

二次多項式の根：

周期連分数を生成する：

異なる式をSqrtで解く：

Sqrt関数からの楕円積分を計算する：

特性と関係  (12)

Sqrt[x]とSurd[x,2]は非負の実数については等しい：

負の実数についてはSqrtは虚数の結果を与えるのに対し実数値のSurdはエラーになる：

平方根の組合せを簡約する：

平方根を含むベキ級数を評価する：

変数が実数値であると仮定して複素平方根を展開する：

係数に平方根を持つ多項式を因数分解する：

Simplifyは平方根を含む式を扱うことができる：

任意の複素引数について平方根を扱う際には多くの微妙な問題が含まれる：

PowerExpandは平方根を含む形式を展開する：

一般にすべての変数が正であると仮定される：

整数の有限和と整数の平方根は代数的数である：

分枝切断線の原因となる極限値を取る：

SqrtはDifferentialRootとして表すことができる：

Sqrtの母関数：

考えられる問題  (3)

平方根は負の実軸に沿った分枝切断線で不連続となる：

Sqrt[x^2]を自動的に x に簡約することはできない：

x が正であると仮定すると，簡約することができる：

PowerExpandを使って形式的に簡約する：

分枝切断線に沿ったところでは以下の値は同じではない：

おもしろい例題  (2)

GoldenRatioへの近似：

平方根のリーマン(Riemann)面：

Wolfram Research (1988), Sqrt, Wolfram言語関数， https://reference.wolfram.com/language/ref/Sqrt.html （1996年に更新）.

テキスト

Wolfram Research (1988), Sqrt, Wolfram言語関数， https://reference.wolfram.com/language/ref/Sqrt.html （1996年に更新）.

CMS

Wolfram Language. 1988. "Sqrt." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1996. https://reference.wolfram.com/language/ref/Sqrt.html.

APA

Wolfram Language. (1988). Sqrt. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Sqrt.html

BibTeX

@misc{reference.wolfram_2024_sqrt, author="Wolfram Research", title="{Sqrt}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Sqrt.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sqrt, organization={Wolfram Research}, title={Sqrt}, year={1996}, url={https://reference.wolfram.com/language/ref/Sqrt.html}, note=[Accessed: 22-November-2024 ]}