FullInformationOutputRegulator

FullInformationOutputRegulator[sys,rspec]

gives the full state information output regulator for sys using specification rspec.

FullInformationOutputRegulator[{sys,{out1,…},{in1,…}},…]

specifies the regulated outputs outi and the controlled inputs inj.

Details and Options

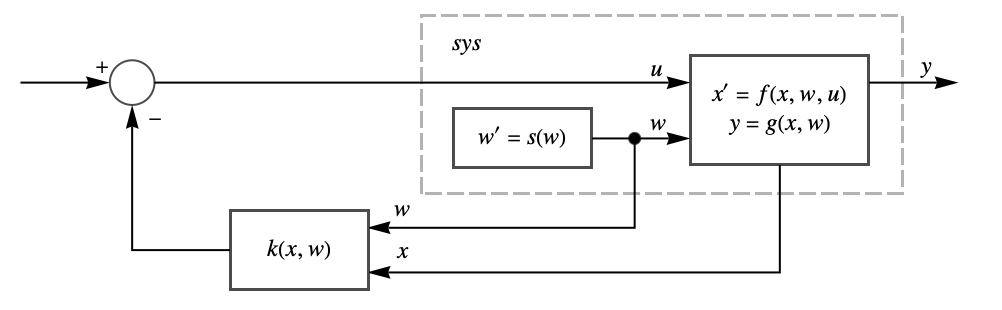
  • FullInformationOutputRegulator returns a regulator that drives the sys outputs to zero and is typically used to suppress or track known inputs to the system.
  • The system sys is taken to have state equations 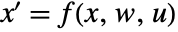and 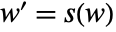and outputs 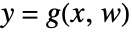, with 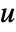being the controllable input. The state 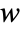is not affected by the input 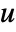and is used to model signals to suppress or track, as indicated by the output function .
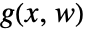  • Typical output functions 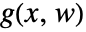, which the regulator will drive to zero:
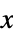
  • suppress the effects of 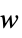on the states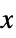
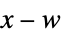
    cause 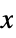to track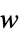
  • The system sys can be StateSpaceModel, AffineStateSpaceModel, or NonlinearStateSpaceModel.
  • The computed state feedback 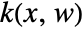regulates sys about an operating point using .
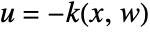  • The state feedback 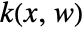has the form 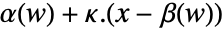, where 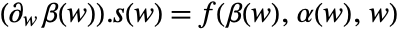, , 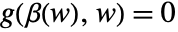and 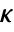is computed following rspec.
  • Possible regulator specifications rspec:
  • {"Poles",{p1,…}}computed with StateFeedbackGains
    {"Weights",{p,…}}computed with LQRegulatorGains
    {"Gains",κ}explicitly given gains
  • With the specification {"method",pars,opts}, the options opts are passed to the gain computation function.
  • The outputs {out1,…} and inputs {in1,…} are part specifications and by default are taken to be All.

Examples

open allclose all

Basic Examples  (1)

Compute the regulating feedback for a system with a constant disturbance of 0.5:

The regulator is a function of the states and the disturbance state :

The closed-loop system:

The output is regulated to zero:

Scope  (8)

The regulator for a linear system with the exosystem pole at the origin:

The closed-loop system:

The exosystem has a pair of complex poles:

The closed-loop system:

The exosystem's states are part of the regulator:

The closed-loop system:

The response:

The system is regulated if pf is negative:

Regulate an AffineStateSpaceModel:

Regulate a NonlinearStateSpaceModel:

Specify the regulated outputs and feedback inputs:

Use LQRegulatorGains to compute the stabilizing gains by specifying the weights:

Specify the gains to use:

Applications  (6)

Reject a disturbance modeled as :

The full model of the system with disturbance:

The regulator:

The closed-loop system:

The output is regulated in the presence of the disturbance:

Track an input modeled as :

The full model of the system and input model:

The regulator:

The closed-loop system:

The output tracks the input:

Simultaneously track a step input and reject a sinusoidal disturbance:

The complete system:

Obtain the regulator:

The closed-loop system:

The simulation shows the output tracking a step signal:

Regulate an aircraft's longitudinal dynamics in the presence of disturbances:»

The disturbances consist of two frequency components:

The complete system:

A control law that regulates the output (speed) in the presence of the disturbances:

The closed-loop system:

Simulation showing regulation being achieved:

The control effort:

Regulate a Rössler prototype-4 system:»

Its chaotic behavior:

The complete model such that the state is regulated and kept constant:

A feedback law:

The closed-loop system:

Simulations show that is regulated and the system has no chaotic behavior with feedback:

Regulate the voltage in a Chua circuit to follow a sinusoid while rejecting a disturbance that is the output of another Chua circuit:»

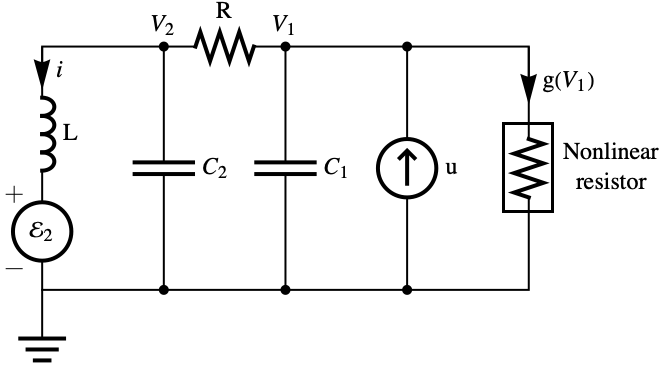
The affine model of the Chua circuit where the nonlinearity is a cubic polynomial:

The exosystem, where ω is the frequency of the sinusoid to be tracked:

The complete system:

The poles of the disturbance model:

The system poles consist of the three new poles and the stabilizable poles:

The regulator:

The closed-loop system:

The simulation shows that the regulation is achieved:

Properties & Relations  (4)

StateFeedbackGains is a special case:

LQRegulatorGains is a special case:

Obtain the closed-loop system using SystemsModelStateFeedbackConnect:

Output regulation is achieved:

Wolfram Research (2014), FullInformationOutputRegulator, Wolfram Language function, https://reference.wolfram.com/language/ref/FullInformationOutputRegulator.html.

Text

Wolfram Research (2014), FullInformationOutputRegulator, Wolfram Language function, https://reference.wolfram.com/language/ref/FullInformationOutputRegulator.html.

CMS

Wolfram Language. 2014. "FullInformationOutputRegulator." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FullInformationOutputRegulator.html.

APA

Wolfram Language. (2014). FullInformationOutputRegulator. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FullInformationOutputRegulator.html

BibTeX

@misc{reference.wolfram_2025_fullinformationoutputregulator, author="Wolfram Research", title="{FullInformationOutputRegulator}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/FullInformationOutputRegulator.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_fullinformationoutputregulator, organization={Wolfram Research}, title={FullInformationOutputRegulator}, year={2014}, url={https://reference.wolfram.com/language/ref/FullInformationOutputRegulator.html}, note=[Accessed: 18-April-2025 ]}