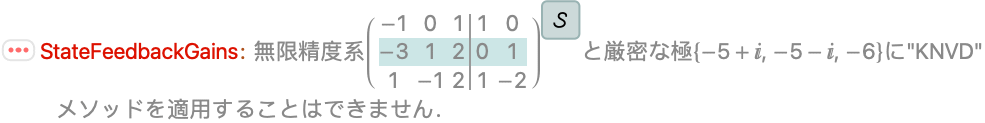StateFeedbackGains
StateFeedbackGains[sspec,{p1,…,pn}]
閉ループ系の極を piに置くような状態指定 sspec の状態フィードバックゲインを与える.
StateFeedbackGains[…,"prop"]
特性"prop"の値を与える.
詳細とオプション


- StateFeedbackGainsは極配置ゲインあるいは固有値の配置としても知られている.
- StateFeedbackGainsは,調整コントローラまたは追跡コントローラを計算するために使われる.
- StateFeedbackGainsは閉ループ系の極を位置 piに変更することで動作する.
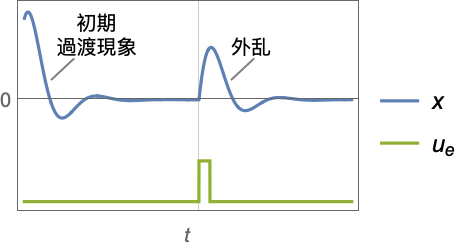
- 調整コントローラは系を押し出そうとする外乱
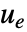 にもかかわらず,系を平衡状態に保とうとする.典型的な例として,倒立振子を直立位置に保つことや航空機の水平飛行を保つこと等がある.
にもかかわらず,系を平衡状態に保とうとする.典型的な例として,倒立振子を直立位置に保つことや航空機の水平飛行を保つこと等がある. - 調整コントローラは
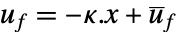 の形式の制御法則で与えられる.ただし,
の形式の制御法則で与えられる.ただし,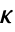 は計算されたゲイン行列である.
は計算されたゲイン行列である. - 置くべき極の数 n は系 sys のSystemsModelOrderで与えられる.
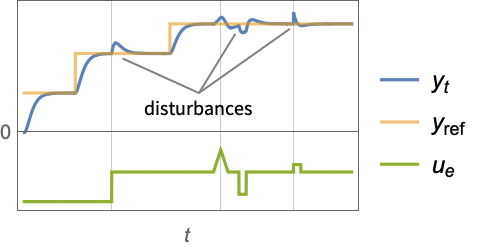
- 追跡コントローラは干渉する外乱
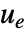 があっても参照信号を追跡しようとする.典型的な例として,車のクルーズコントロールやロボットの経路追跡がある.
があっても参照信号を追跡しようとする.典型的な例として,車のクルーズコントロールやロボットの経路追跡がある. - 追跡コントローラは
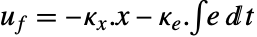 の形の制御法則によって与えられる.ただし,
の形の制御法則によって与えられる.ただし,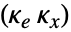 は系 sys と
は系 sys と 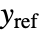 のダイナミクスを含む拡張された系の計算されたゲイン行列である.
のダイナミクスを含む拡張された系の計算されたゲイン行列である. - 置くべき極の数 n は
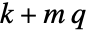 で与えられる.ただし,
で与えられる.ただし,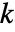 は sys の SystemsModelOrderで,
は sys の SystemsModelOrderで,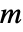 は yrefの次数で,
は yrefの次数で, 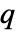 は信号 yrefの数で与えられる.
は信号 yrefの数で与えられる. - 極の配置設計はStateSpaceModelで指定されるような線形系に使うことができる.
-
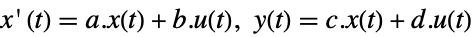
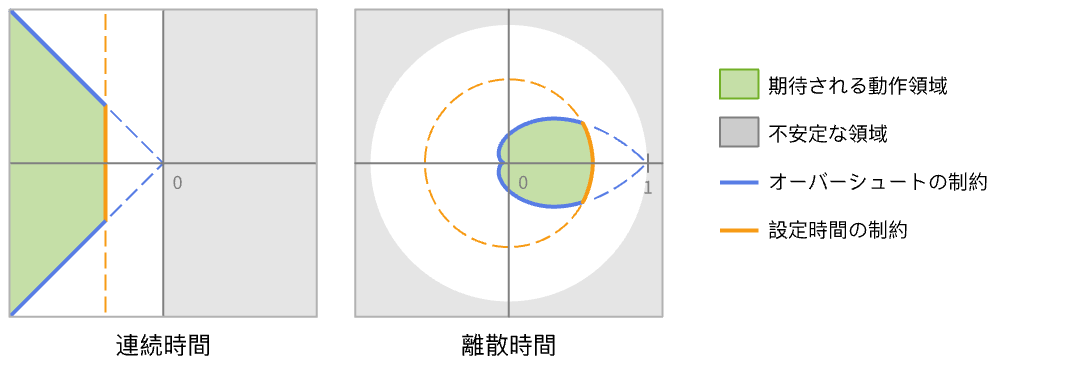
連続時間系 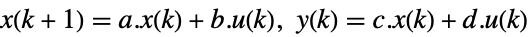
離散時間系 - 結果の閉ループ系 csys のパフォーマンスは主に極 piの位置によって決まる.
- 通常,整定時間等のパフォーマンスの制約とオーバーシュート等の品質の制約がある.これらは望ましい極位置である特定の領域に対応する.
- 系の指定 sspec は sys と uf,yt,yrefの指定である.
- 系の指定 sspec は以下の形でよい.
-
StateSpaceModel[…] 線形制御入力と線形状態 AffineStateSpaceModel[…] 線形制御入力と非線形状態 NonlinearStateSpaceModel[…] 非線形制御入力と非線形状態 SystemModel[…] 一般的な系のモデル <…> Associationとして与えられる詳細な系の指定 - 系の指定の詳細は次のキーを持つことができる.
-
"InputModel" sys モデルの任意のもの "FeedbackInputs" All フィードバック入力 uf "TrackedOutputs" None 追跡された出力 yt "TrackedSignal" Automatic yrefのダイナミクス - 追跡された信号のダイナミクスは参照信号と時間変数の関数として与えられ,デフォルトで,一定しているとみなされる.
-
Function[{r, t},r'[t]] 連続時間系 Function[{r,k},r[k+1]-r[k]] 離散時間系 - フィードバック入力と追跡された出力は次の形でよい.
-
{num1,…,numn} StateSpaceModel,AffineStateSpaceModel,NonlinearStateSpaceModelで使われる番号付きの入力 numi {name1,…,namen} SystemModelで使われる名前付きの入力 namei All すべての入力を使う - AffineStateSpaceModel,NonlinearStateSpaceModel,SystemModelのような非線形系については, 系は保存された動作点の周りで線形化される.
- StateFeedbackGains[…,"Data"]は,cd["prop"]の形で追加的な特性の抽出に使えるSystemsModelControllerDataオブジェクト cd を返す.
- StateFeedbackGains[…,"prop"]を使って cd["prop"]の値を直接得ることができる.
- 次は,特性"prop"の可能な値である.
-
"ClosedLoopPoles" 線形化された"ClosedLoopSystem"の極 "ClosedLoopSystem" 系 csys {"ClosedLoopSystem", cspec} 閉ループ系の形に対する詳細な制御 "ControllerModel" モデル cm "Design" コントローラ設計のタイプ "DesignModel" 設計に使われるモデル "FeedbackGains" ゲイン行列 κ またはそれに相当するもの "FeedbackGainsModel" モデル gm あるいは{gm1,gm2} "FeedbackInputs" フィードバックに使われる sys の入力 uf "InputModel" 入力モデル sys "InputCount" sys の入力 u の数 "OpenLoopPoles" "DesignModel"の極 "OutputCount" システムの出力 y の数 "SamplingPeriod" sys のサンプリング周期 "StateCount" sys の状態 x の数 "TrackedOutputs" 追跡された sys の出力 yt - 次は,cspec の可能なキーである.
-
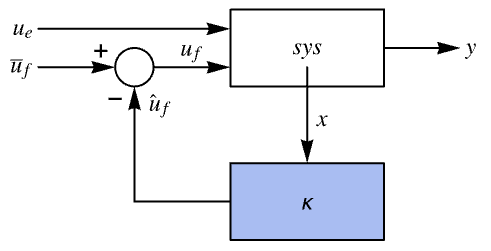
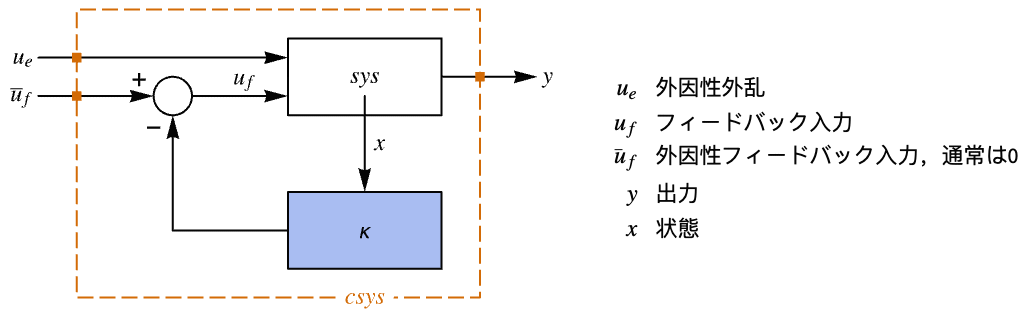
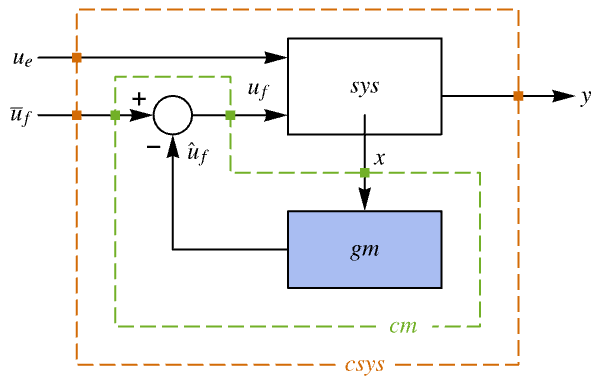
"InputModel" csys の入力モデル "Merge" csys をマージするかどうか "ModelName" csys の名前 - 次は,調整器のレイアウトの図である.
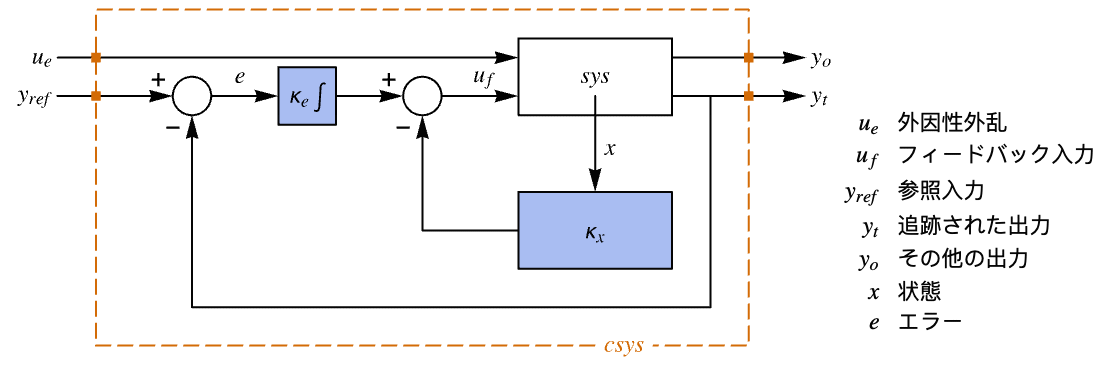
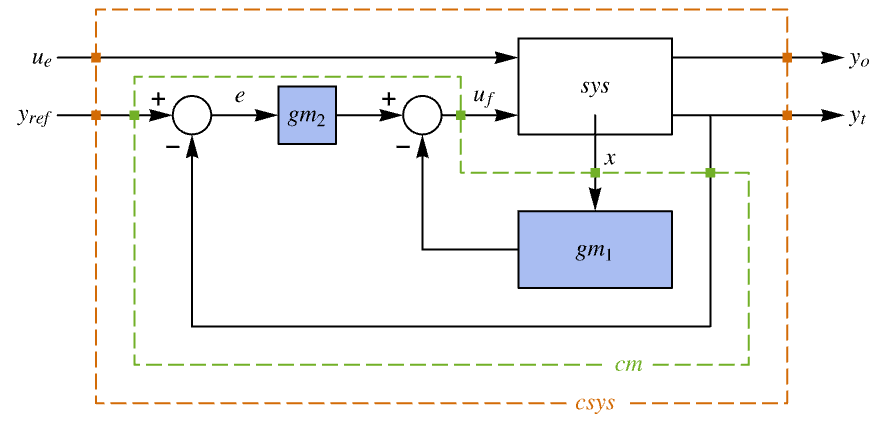
- 次は,追跡器のレイアウトの図である.
- StateFeedbackGainsは以下の設定のMethodオプションを取る.
-
Automatic メソッドの自動選択 "Ackermann" Ackermann法 "KNVD" Kautsky–Nichols–Van Dooren法
例題
すべて開くすべて閉じる例 (3)
スコープ (32)
工場モデル (6)
連続時間StateSpaceModel:
離散時間StateSpaceModel:
ディスクリプタStateSpaceModel:
作用点がないAffineStateSpaceModelは0であるとみなされる:
作用点がないNonlinearStateSpaceModelは0であるとみなされる:
特性 (10)
StateFeedbackGainsはデフォルトでフィードバックゲインを返す:
追跡 (5)
オプション (6)
Method (6)
デフォルトで,厳密値または記号値を持つ系には"Ackermann"メソッドが使われる:
厳密ではない系には,デフォルトで,"KNVD"メソッドが使われる:
少なくとも状態と同じだけの入力がある非厳密系にはLinearSolveが使われる:
"Ackermann"メソッドでは多重入力系に対して1つの入力しか使われない:
アプリケーション (14)
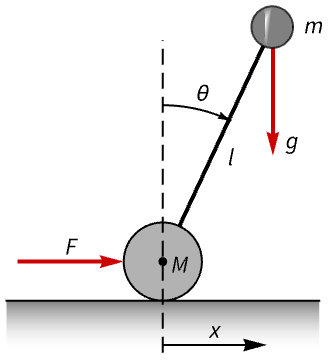
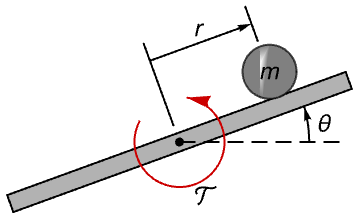
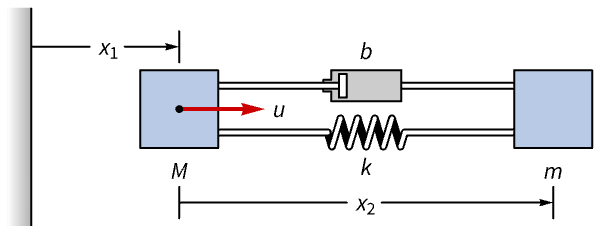
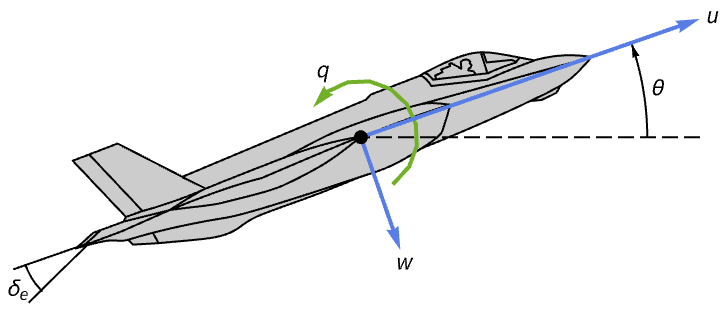
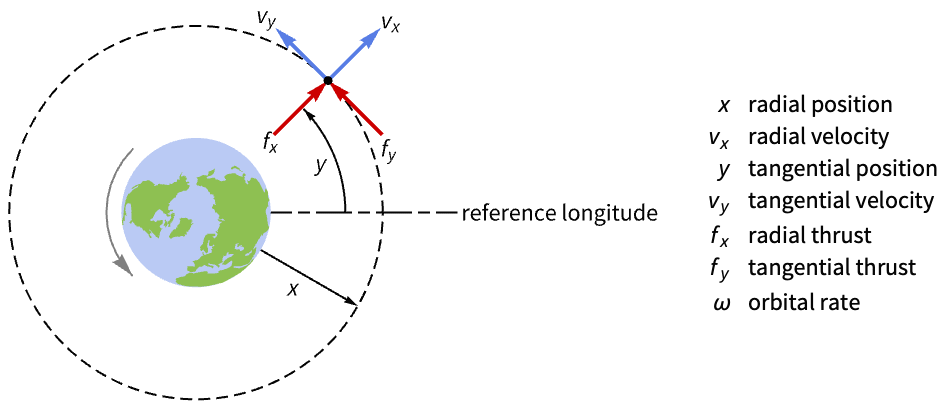
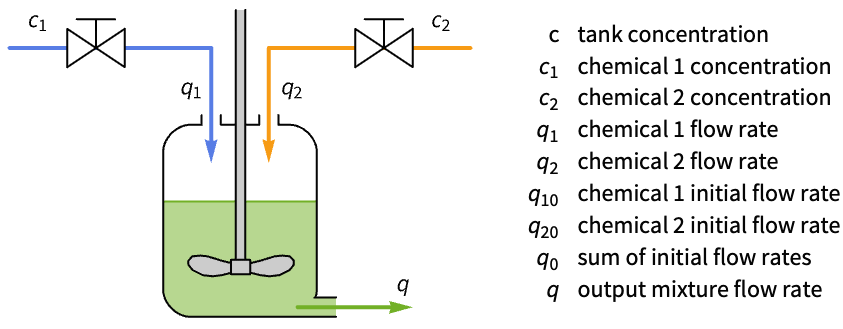
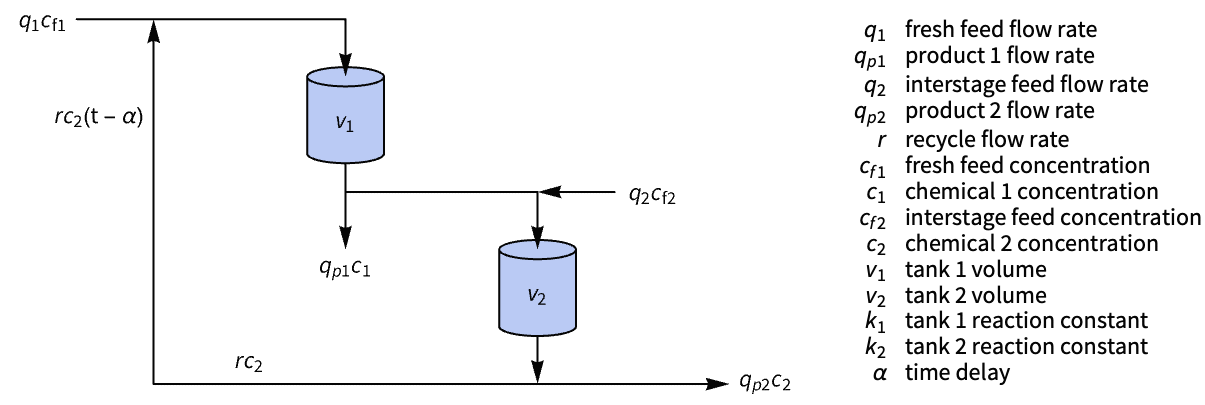
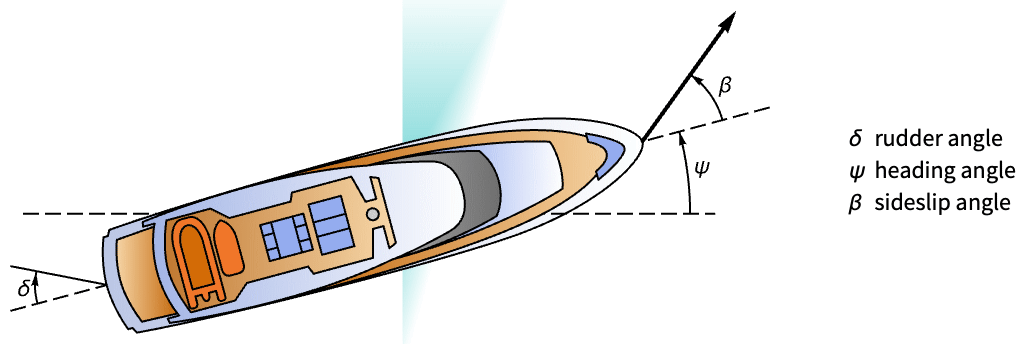
力学系 (4)
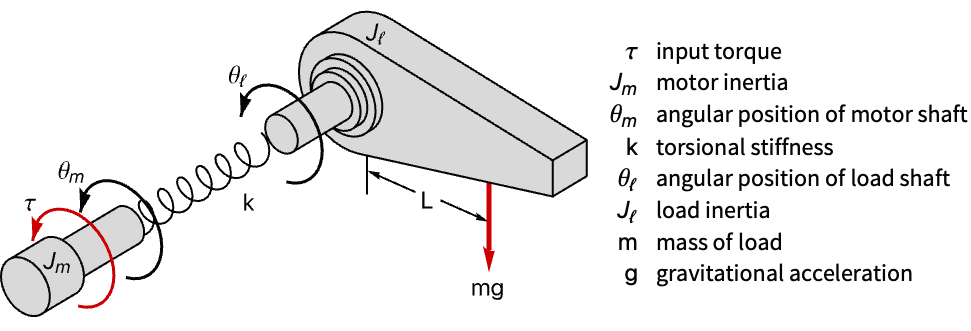
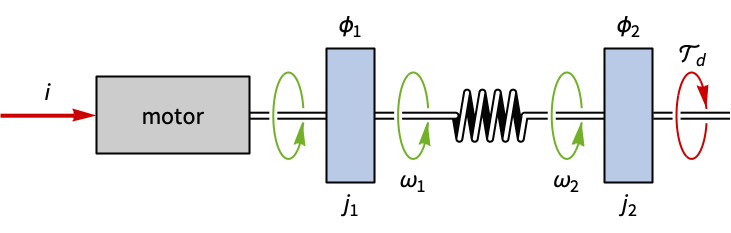
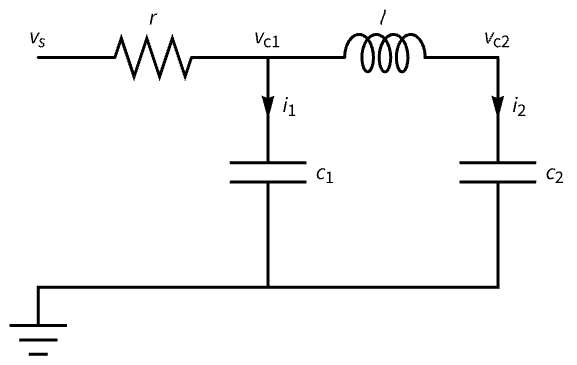
電気機械系 (1)
デッドビート制御 (1)
特性と関係 (17)
状態フィードバックゲインは負のフィードバックについて計算される:
制御努力は閉ループ極が開ループ極から離れるにつれて大きくなる:
制御可能な標準StateSpaceModelの極はすべて状態フィードバックを使って制御できる:
制御可能な非特異ディスクリプタStateSpaceModelの極もすべて制御できる:
制御不可能な標準StateSpaceModelの部分系のみが制御可能である:
非特異ディスクリプタの遅い部分系の制御可能な極だけが制御できる:
遅い部分系の極は希望の位置に移動され,速い部分系に対応する![]() における極は変化しない:
における極は変化しない:
非特異ディスクリプタの制御可能な遅い部分系の極はどれも制御できない:
LQRegulatorGainsとStateFeedbackGainsは単一入力の系に対して同じ結果を返す:
LQRegulatorGains設計の閉ループ曲があるStateFeedbackGains:
LQRegulatorGainsは同じゲインを与える:
![]() ρ c.c x(t)2+u(t)2t を最小化する閉ループ極は対称根軌跡プロットを使って得ることができる:
ρ c.c x(t)2+u(t)2t を最小化する閉ループ極は対称根軌跡プロットを使って得ることができる:
LQRegulatorGainsを使っても同じゲインが得られる:
StateSpaceModelについては,StateFeedbackGainsとFullInformationOutputRegulatorは同じ結果を与える:
推定器調整器は状態フィードバック行列と推定器ゲイン行列を使って組み立てられる:
単一入力系の閉ループ系におけるゲインに相当する状態フィードバックゲイン:

この実現について,状態フィードバックゲインは{{κ,0,…,0}}の形である:
この実現について,状態フィードバックゲインは{{κ,0,…,0}}の形である:
状態フィードバックと推定器ゲインは互いに互いのデュアルである:
状態フィードバックゲイン行列は推定器ゲイン行列の共役転置であり,逆もまた真である:
状態フィードバックは系の入力ブロッキング特性を変えはしない:
開ループ系も閉ループ系も入力Sin[2t]をブロックする:
テキスト
Wolfram Research (2010), StateFeedbackGains, Wolfram言語関数, https://reference.wolfram.com/language/ref/StateFeedbackGains.html (2021年に更新).
CMS
Wolfram Language. 2010. "StateFeedbackGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/StateFeedbackGains.html.
APA
Wolfram Language. (2010). StateFeedbackGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateFeedbackGains.html