WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

StateResponse
✖
StateResponse

✖
StateResponse[sys,u,{t,tmin,tmax}]

gives the numeric state response of the state-space model sys to input u for tmin≤t≤tmax.

✖
StateResponse[sys,{u[0],u[1],…}]

gives the response of the discrete-time state-space model sys to the input sequence u[i].

✖
StateResponse[sys,u,t]

gives the symbolic state response as a function of time t.

✖
StateResponse[sys,{u1,…,um},…]

gives the state response for multiple inputs ui.

✖
StateResponse[{sys,{x10,x20,…,xn0}},…, …]

gives the response with initial states xi0.

Details

  • StateResponse solves the state differential or difference equations for the given input u.
  • The state-space model sys can be a StateSpaceModel, a continuous-time AffineStateSpaceModel, or a continuous-time NonlinearStateSpaceModel.
  • A linear StateSpaceModel sys can also be a descriptor and delay system.
  • The initial states xi0 are taken to be the state operating values of sys unless specified.
  • For descriptor systems, the initial states need to be consistent.
  • For delay systems, the initial states include history and can be given as xi0[t] for t≤0. »

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

The state response of a continuous-time system to a unit step input:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-50qh2f
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-xwienr
Out[2]=2

The response of a discrete-time system with initial conditions {1,-1}:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-kqmx6a
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-vbrbt0
Out[2]=2

The state-response of a system to a Dirac delta input:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-kd0lff
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-ozthqy
Out[2]=2

The step response of a time-delay system:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-enqqej
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-lh51s
Out[2]=2

Scope  (26)Survey of the scope of standard use cases

Continuous-Time Systems  (16)

The state response of a single-input system to a unit step:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-scesh6
Out[1]=1

The initial conditions are assumed to be zero:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-9fei9h
Out[2]=2

The state response for a generic continuous-time system:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-840t2
Out[1]=1

The response to a unit step input:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-ulo3
Out[1]=1

The response of a descriptor StateSpaceModel:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-tjrx4p
Out[1]=1

With an algebraic equation:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-fvws2s
Out[1]=1

The numeric response to a sinusoidal input:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-rotz0k
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-x3bo6p
Out[2]=2

Specify {0.2,0.1} as the initial state values:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-p0viva
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-3xncix
Out[2]=2

The response of a two-input system to input signals {SquareWave[t],Sin[t]}:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-5p9fve
Out[1]=1

The state response of a three-input system to inputs {Sin[t],Cos[t],Cos[t]}:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-vm2pfi
Out[1]=1

Plot the response:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-iucpm9
Out[2]=2

If there are fewer input signals than inputs, the remaining inputs are assumed to be zero:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-0yxs3i
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-59ahqf
Out[2]=2

If a scalar input signal is given for a multiple-input system, it is applied to each input in turn:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-habbfs
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-lasudb
Out[2]=2

StateResponse[…,{t,tmin,tmax}] gives the result in terms of interpolating function objects:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-bfrc6w
Out[1]=1

Plot the response:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-l7kecd
Out[2]=2

The step response of a singular descriptor system:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-h2wuyk
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-lr1l0s
Out[2]=2

The symbolic response for a singular descriptor system:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-qfg82
Out[1]=1

Plot the response:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-indaxy
Out[2]=2

The state response of an AffineStateSpaceModel to a UnitStep input:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-4ooqbv
Out[1]=1

Plot the response:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-vpv6nm
Out[2]=2

The response from nonzero initial conditions:

In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-qqzq1k
Out[3]=3

The state response of a NonlinearStateSpaceModel to a sinusoidal input:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-1i33z2
Out[1]=1

Plot the response:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-j7031r
Out[2]=2

Discrete-Time Systems  (10)

The state response of a single-input system to a unit step input:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-c382p8
Out[2]=2

Plot the response for eight steps:

In[6]:=6
✖
https://wolfram.com/xid/01ykmm5x0vy-06rw4e
Out[6]=6

The response for a generic discrete-time system:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-n23rsa
Out[1]=1

The response to a unit step sequence:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-i5i745
Out[1]=1

The response for a symbolic descriptor system:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-chq17
Out[1]=1

The state response to a sampled sinusoid:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-l62xmk
Out[1]=1

Plot the response with a zero-order hold:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-77ptsd
Out[2]=2

The state response of a two-input system to two randomly sampled inputs:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-720hnr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-0omx4
Out[2]=2

The response to a random input sequence:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-ys8a9x
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-l3twk8
Out[2]=2

A two-input state-space model:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-ixjgt5

When only one input signal is given, the remaining inputs are set to zero:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-dqr8so
Out[2]=2

The second and fourth states are not excited because the second input is zero:

In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-r5bmqw
Out[3]=3

If a single-input sequence is given to a multi-input system, it is applied to each input in turn:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-38fkx

Discrete-time time-delay systems accept a history for time steps before k0:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-dic56t
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-i2f5qb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-g1ickg
Out[3]=3

Generalizations & Extensions  (3)Generalized and extended use cases

If the initial time is not specified, it is assumed to be zero:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-x8dm9
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-fzwokp
Out[2]=2

For a state-delay system, the initial states can include history:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-bxz4vh
Out[1]=1

For discrete-time systems with delays, the initial states can be given as a sequence:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-hnefhc
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-l6jvx8
Out[2]=2

Applications  (4)Sample problems that can be solved with this function

The model of a stabilized inverted pendulum on a moving cart has the cart displacement d and velocity v, together with the pendulum's angular position θ and velocity ω as the state variables:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-ua0byb

Compute the acceleration a of the cart and the angular acceleration α of the pendulum by differentiating the cart's velocity and the pendulum's angular velocity obtained using StateResponse:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-pbqyfn
Out[3]=3
Out[4]=4

Plot the results:

In[5]:=5
✖
https://wolfram.com/xid/01ykmm5x0vy-gbq946
Out[5]=5

Analyze the response of the states to each control input for a multi-input system:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-0oienu
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-e2sm72
Out[2]=2

The state-space model of a production and inventory control system with desired production rate and sales rate as inputs and actual production rate and inventory level as states:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-es0ry0

Determine the response for a given production rate and 10% jump in sales from the initial equilibrium condition:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-s9hifn
Out[2]=2

Plot the response for specific initial conditions:

In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-262fe2
Out[3]=3

The Clohessy–Wiltshire equations model the relative motion between two satellites orbiting a central body:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-p98pk

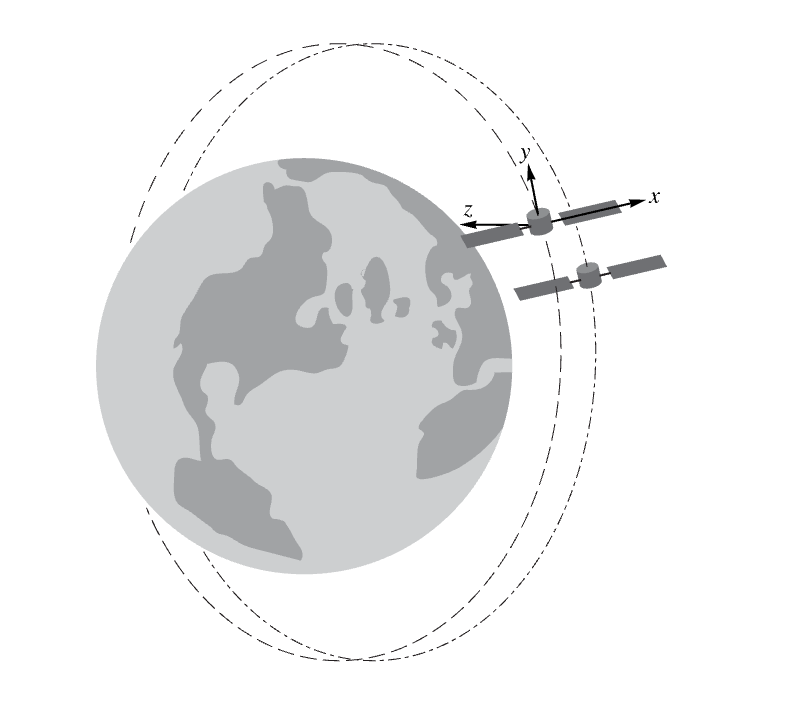
Use StateResponse to obtain the closed relative orbits from a particular set of launch conditions:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-gj3mb0
In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-kq2yop
Out[3]=3

Properties & Relations  (3)Properties of the function, and connections to other functions

The results of StateResponse and OutputResponse match for state output:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-xsst8y
Out[2]=2

State output occurs when the output matrix is identity and the transmission matrix is zero:

In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-308m0r
Out[3]=3

The natural response is determined by the poles of the system:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-4ggyzq
Out[1]=1

It is invariant under any similarity transformation:

In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-kc3y9j
Out[2]=2

The original states:

In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-c2q5kh
Out[3]=3

The initial states for a descriptor system are chosen to be consistent for the inputs:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-huclh
In[2]:=2
✖
https://wolfram.com/xid/01ykmm5x0vy-knj6o
Out[2]=2

The second state equals the derivative of the input:

In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-r2c57
Out[3]=3

When inconsistent conditions are given, they are replaced:

In[4]:=4
✖
https://wolfram.com/xid/01ykmm5x0vy-e1l7za
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/01ykmm5x0vy-klh2ji
Out[5]=5

Consistent initial states depend on the slow subsystem in KroneckerModelDecomposition:

In[6]:=6
✖
https://wolfram.com/xid/01ykmm5x0vy-624bj
Out[6]=6

For continuous-time systems, the initial conditions are given by :

In[7]:=7
✖
https://wolfram.com/xid/01ykmm5x0vy-i46028
Out[7]=7

Possible Issues  (2)Common pitfalls and unexpected behavior

Symbolic state responses do not support time delays:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-erfy8
Out[2]=2

Try a numeric simulation:

In[3]:=3
✖
https://wolfram.com/xid/01ykmm5x0vy-ce9uu3
Out[4]=4

For descriptor systems, solutions only exist when Det[λ e - a]≠0 for some λ:

In[1]:=1
✖
https://wolfram.com/xid/01ykmm5x0vy-hfa3f1
Out[1]=1
Wolfram Research (2010), StateResponse, Wolfram Language function, https://reference.wolfram.com/language/ref/StateResponse.html (updated 2014).
✖
Wolfram Research (2010), StateResponse, Wolfram Language function, https://reference.wolfram.com/language/ref/StateResponse.html (updated 2014).

Text

Wolfram Research (2010), StateResponse, Wolfram Language function, https://reference.wolfram.com/language/ref/StateResponse.html (updated 2014).

✖
Wolfram Research (2010), StateResponse, Wolfram Language function, https://reference.wolfram.com/language/ref/StateResponse.html (updated 2014).

CMS

Wolfram Language. 2010. "StateResponse." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/StateResponse.html.

✖
Wolfram Language. 2010. "StateResponse." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/StateResponse.html.

APA

Wolfram Language. (2010). StateResponse. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateResponse.html

✖
Wolfram Language. (2010). StateResponse. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateResponse.html

BibTeX

@misc{reference.wolfram_2025_stateresponse, author="Wolfram Research", title="{StateResponse}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/StateResponse.html}", note=[Accessed: 29-March-2025 ]}

✖
@misc{reference.wolfram_2025_stateresponse, author="Wolfram Research", title="{StateResponse}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/StateResponse.html}", note=[Accessed: 29-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_stateresponse, organization={Wolfram Research}, title={StateResponse}, year={2014}, url={https://reference.wolfram.com/language/ref/StateResponse.html}, note=[Accessed: 29-March-2025 ]}

✖
@online{reference.wolfram_2025_stateresponse, organization={Wolfram Research}, title={StateResponse}, year={2014}, url={https://reference.wolfram.com/language/ref/StateResponse.html}, note=[Accessed: 29-March-2025 ]}